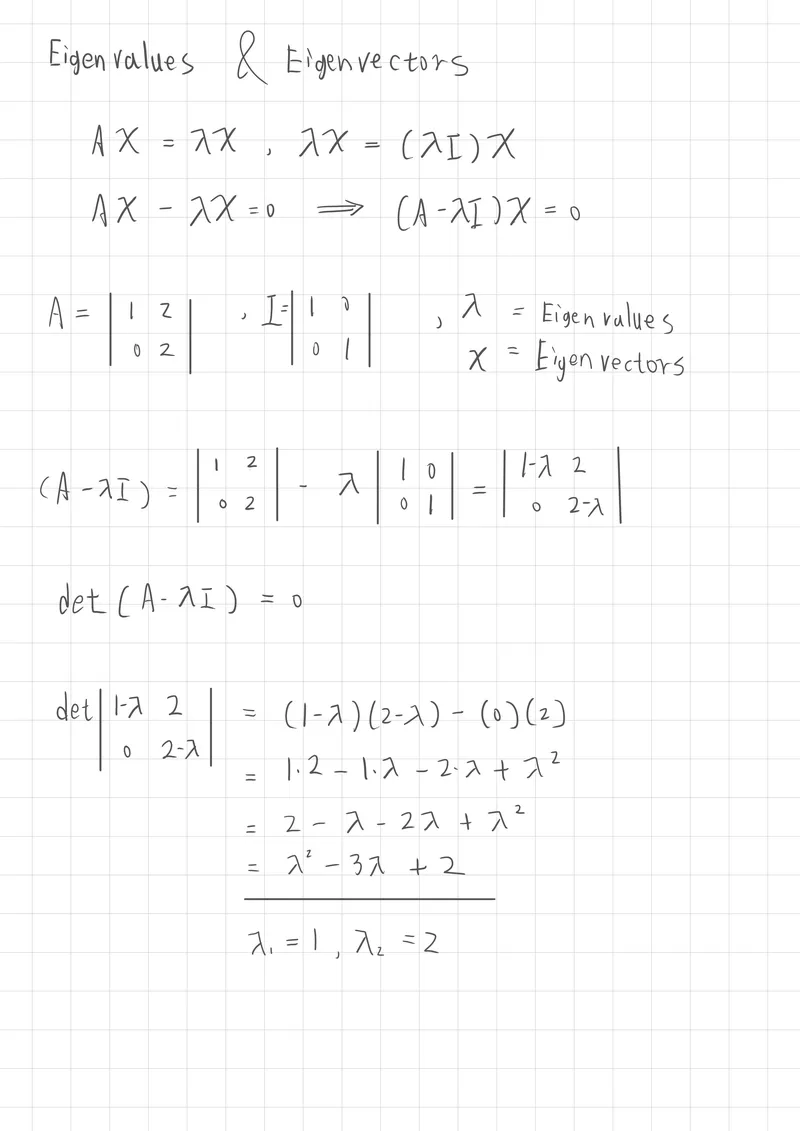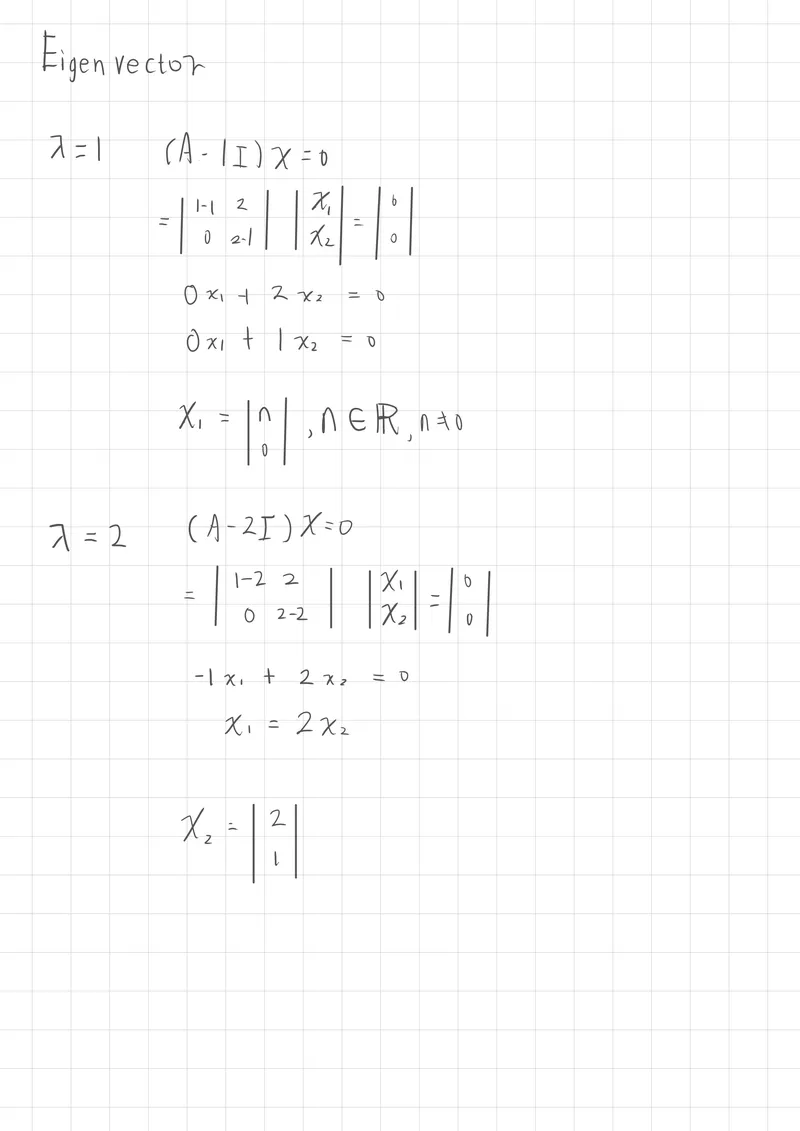計算機應用數學-線性代數
前敘
筆記內容著重於,計算機與人工智慧領域所應用的數學,目的為快速導讀數理重點脈絡及公式,類似於直式的心智圖
目錄
筆記目前整理三個部分
- 計算機應用數學-微積分
(研究連續變化、累積與極限現象的數學)
- 計算機應用數學-線性代數
(研究向量、矩陣與線性變換的結構與操作)
- 計算機應用數學-離散數學(和廣義邏輯學)
(研究離散結構的數學,為計算理論與邏輯基礎)
矩陣向量特性
行矩陣(Row Matrix / vector)
A=[a11a12a13]
列矩陣(Column Matrix / vector)
A=a11a21a31
單元素矩陣(Singleton Matrix)
A=[a11]
方矩陣(Square Matrix)
指行數和列數相等的矩陣
A=[a11a21a12a22]
全一矩陣(Matrix of Ones)
O=111111111
零矩陣(Zero Matrix)
A=[0000]
單位矩陣(Identity Matrix, I)
單位矩陣是一種方陣,其主對角線元素為 1,其他元素為 0
A=[1001]
對角矩陣(Diagonal Matrix)
對角矩陣是一種方陣,主對角線以外的元素為 0
A=d1000d2000d3
上三角矩陣(Upper Triangular Matrix)
A=a1100a12a220a13a23a33
下三角矩陣(Lower Triangular Matrix)
A=a11a21a310a22a3200a33
對稱矩陣(Symmetric Matrix)
A=abcbdecef滿足:A=A⊤
反對稱矩陣(Skew-Symmetric Matrix)
A=0−a−ba0−cbc0滿足:A=−A⊤
矩陣特徵值
對角化 (Diagonalization)
A=P⋅D⋅P−1
- P 是一個由矩陣 A 的特徵向量組成的矩陣。
- D 是一個對角矩陣,其中的對角元素是 A 的特徵值。
- P−1 是矩陣 P 的逆矩陣。
特徵值與特徵向量(Eigenvalues and Eigenvectors)
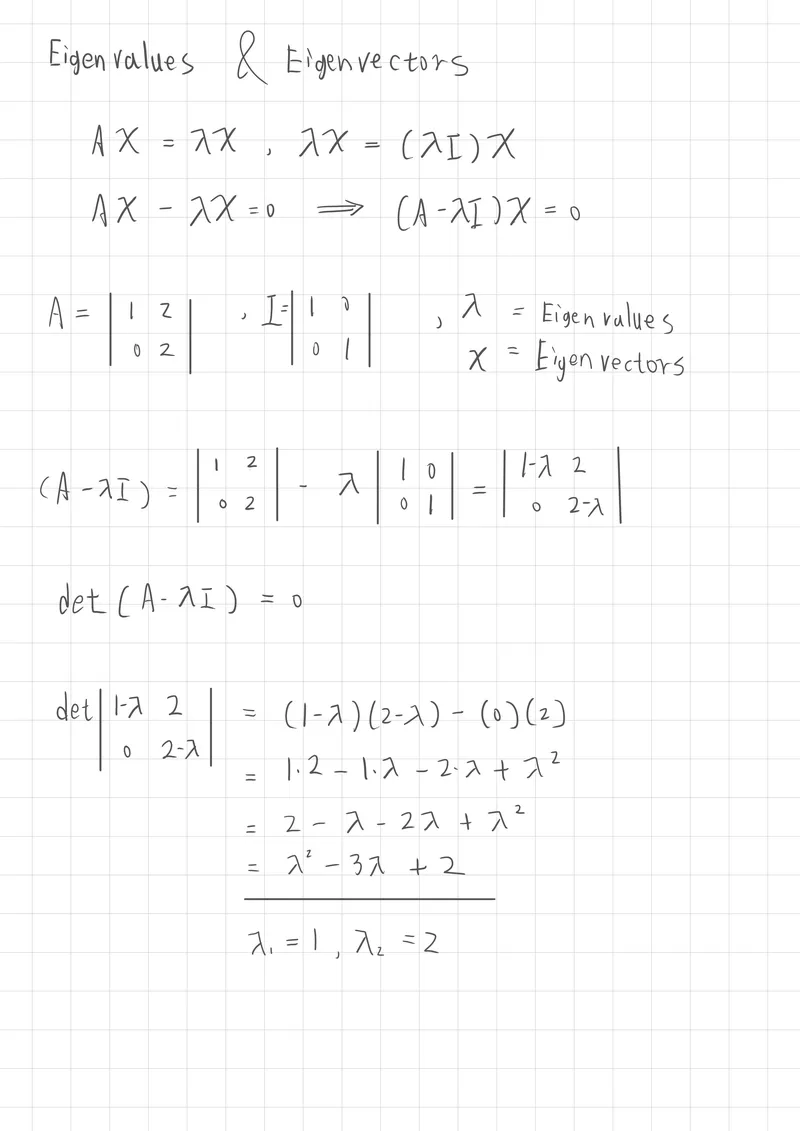
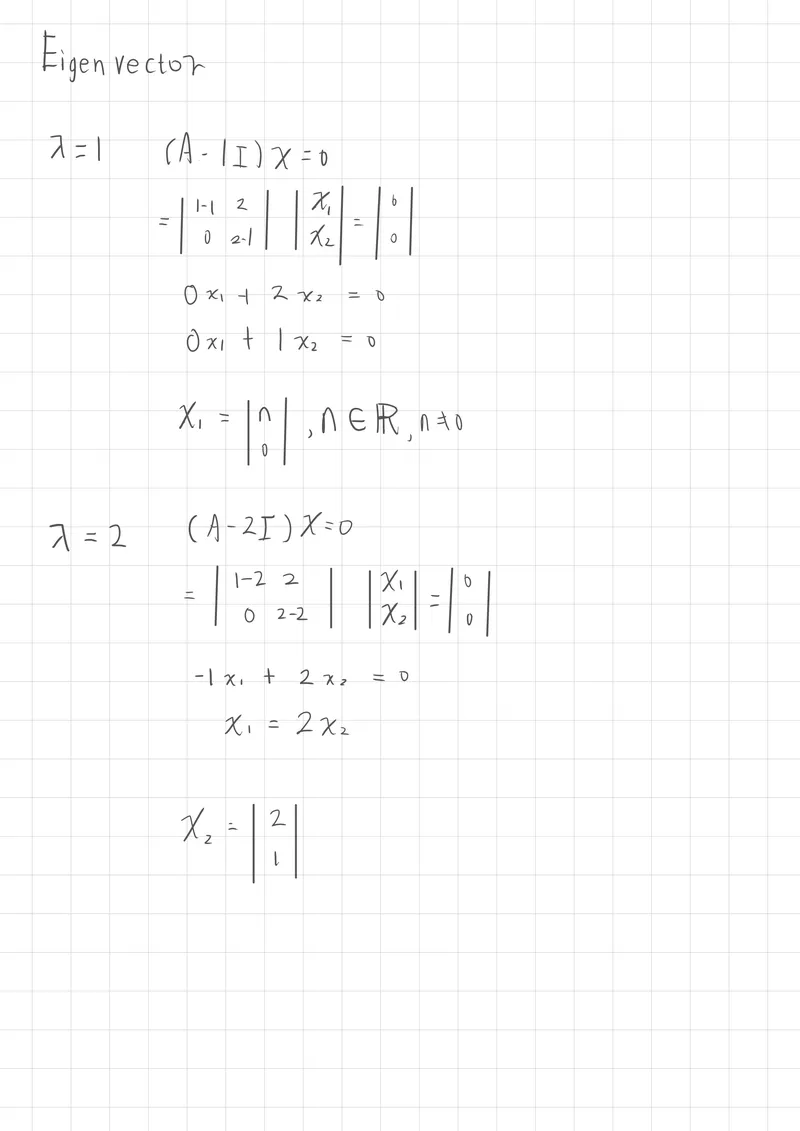
基本運算
矩陣加法(Matrix Addition)
矩陣加法的條件是兩個矩陣的維度必須相同,也就是說,它們的行數和列數必須相等。進行加法運算時,對應位置的元素相加。
A=(1324),B=(5768)
A+B=(1+53+72+64+8)=(610812)
矩陣乘法(Matrix Multiplication)
矩陣乘法不備具交換律,因此乘法順位會影響輸出張量
Am×n⋅Bn×p=Cm×p
A=(1324),B=(5768)
A×B=(1×5+2×73×5+4×71×6+2×83×6+4×8)=(19432250)
例子2:
AB=(x1x2)(y1y2)=(x1y1x2y1x1y2x2y2)
純量乘法(Scalar Multiplication)
純量乘法讓矩陣所代表的變換按比例縮放
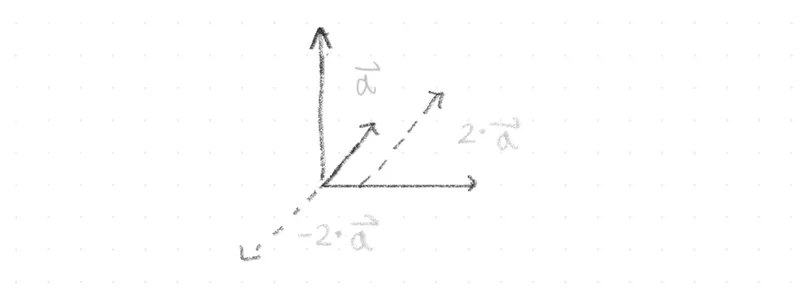
kA=k×(a11a21a12a22)=(ka11ka21ka12ka22)
A=(1324),2×A=(2648)
對稱矩陣 (Symmetric Matrix)
AT=A
表示矩陣轉置(Matrix Transposition)為矩陣本身
例子
aij=aji
A=123245356
A12=A21=2
A13=A31=3
A23=A32=5
重點
- 用於 特徵值分解 (Eigenvalue Decomposition)
- 正交對角化 (Orthogonally Diagonalizable)。
行列式(Determinant, Det)
A=[acbd]
det(A)=ad−bc
拉普拉斯展開(Laplace expansion)
A=a11a21a31a12a22a32a13a23a33
det(A)=a11a22a32a23a33−a12a21a31a23a33+a13a21a31a22a32
需注意交替性(Alternating Property)決定正負號
伴隨矩陣(Adjoint / Adjugate Matrix)
為每個元素求餘子式(Cofactor)後轉置:
adj(A)=[cofactor(A)]⊤
反矩陣(Inverse Matrix)
僅對於方陣(Square Matrix)時才能使用反矩陣
若 A 為可逆矩陣(即 det(A)=0)則
A−1=det(A)1⋅adj(A)
I 是單位矩陣 (Identity Matrix)
AA−1=A−1A=I
對於 A 是 2×2 矩陣:
A=[acbd]
反矩陣公式:
A−1=det(A)1[d−c−ba]
轉置矩陣(Transpose Matrix)
將矩陣的行與列對調:
A⊤=transpose of A
例:
A=[1324]⇒A⊤=[1234]
解線性方程組
克拉默法則(Cramer's Rule)
用於求解線性方程組(System of Linear Equations),當係數矩陣為可逆矩陣(即行列式不為零)時

高斯消去法(Gaussian Elimination)
這種方法透過行運算,將矩陣變成上三角形式,然後用回代法求解。
假設已知方程組:
[2112][x1x2][−12]
將 x1 的係數變為 1
用 第一行除以 2:
[110.52]∣[−0.52]
將 x1 在第二行變為 0
用 第二行 - 第一行 × 1:
[100.51.5]∣[−0.52.5]
回代求解
-
先解 x2 :
1.5x2=2.5⇒x2=1.52.5=35
-
代入 x1 的方程:
x1+0.5×35=−0.5
x1=−0.5−65=−63−65=−68=−34
結果
x1=−34,x2=35
LU 分解
這種方法將矩陣 A 分解為兩個矩陣:
A=LU
- LL 是 下三角矩陣 (Lower Triangular Matrix)
- UU 是 上三角矩陣 (Upper Triangular Matrix)
線性代數
線性方程組(System of Linear Equations | simultaneous equations)
二元一次方程組:
{A1x+B1y=C1A2x+B2y=C2
線性方程組的解法
代入法(Substitution Method)
{x+2y=83x−y=3
-
從第一條方程式中解出 xx:
x=8−2y
-
將 x = 8 - 2y 代入第二條方程式:
3(8−2y)−y=3
解得 y=1y = 1。
-
把 y = 1 代入x = 8 - 2y 得到 x=6
解: x=6x = 6, y=1y = 1
加減法(Elimination Method)
{2x+3y=124x−2y=6
-
使 y 消失。首先將第一條方程式乘以 2,第二條方程式乘以 3,然後兩式相加:
4x+6y=2412x−6y=18
-
相加兩條方程式:
(4x+6y)+(12x−6y)=24+1816x=42⇒x=1642=821
-
將 x=821 代入原方程式2x+3y=12,得到:
2×821+3y=12⇒842+3y=12
y=814=47
解: x=821,y=47
矩陣法(Matrix Method)
矩陣法適用於更高維度的線性方程組,這種方法使用矩陣來表示方程組,並通過矩陣運算來求解。這在計算機科學和數值分析中非常常見。
步驟:
- 將方程組寫成矩陣形式:A⋅X=B,其中 A 是系數矩陣,X 是變數矩陣,B 是常數矩陣。
- 求解 X=A−1⋅B(假設 A 是可逆的)
(a1a2b1b2)(xy)=(c1c2)
(xy)=(a1a2b1b2)−1(c1c2)
範例:
{x+y=42x−y=1
-
寫成矩陣形式:
(121−1)(xy)=(41)
-
求解矩陣:
X=A−1⋅B
計算 A−1,然後計算 X。
線性方程式(Linear Equations)
線性方程式是指 變數的最高次方為 1 的方程式,表示的是線性關係,可以有一個變數、兩個變數或多個變數。例如:
一元一次方程式( Linear equation in one variable):
ax+b=c
這只涉及一個變數 x,解出來是 x = 2。
二元一次方程式(linear equation in two variable ):
這種方程式代表一條 直線,解是無限多個點的集合。
ax+by=c
多元一次方程式( linear equation in multi variable):
關鍵字: **超平面(hyperplane)**方程式、高維度
ax+by+cz=d