單層感知器（Single-Layer Perceptron），用於二分類問題

前續

一個簡單的單層感知器（SLP）模型，用於二分類問題，是神經網路中最基本的結構，可作為後續學習深度神經網路基礎。

開發環境: TensorFlow

理論關鍵字: sigmoid 、binary cross entropy、Stochastic Gradient Descent

完整程式碼

這裡提供本文的完整程式碼供學習使用，可以加入Github收藏，日後有更新都歡迎使用

https://github.com/Rayder-R/System-36-blog-example

目錄

1. 資料準備階段
2. 單層感知器實作

1. 準備資料階段

使用Numpy的隨機常態分佈來做為簡易資料集，

以下主要任務

• 隨機生成資料各100筆
• 合併資料集
• 繪製資料點視覺化

# %% 資料準備
np.random.seed(40)  # 固定隨機種子
class_0 = np.random.randn(100, 2) + np.array([-2, 0])  # 第一類
class_1 = np.random.randn(100, 2) + np.array([2, 0])   # 第二類

print("class_0 shape:", class_0[:1], class_0.shape)
print("class_1 shape:", class_0[:1], class_1.shape)

# 合併資料與標籤
data = np.vstack([class_0, class_1]).astype(np.float32)
labels = np.array([0]*100 + [1]*100).astype(np.float32).reshape(-1, 1)

# 顯示合併後資料與 shape
print("Data set:", data[:1], "shape:", data.shape)
print("Labels set:", labels[:1], "shape:", labels.shape)

# 繪製資料點
plt.scatter(class_0[:, 0], class_0[:, 1],
            alpha=0.7,
            linewidth=0.1,
            s=40,
            color='#003060',
            label='Class 0'
            )
plt.scatter(class_1[:, 0], class_1[:, 1],
            alpha=0.3,
            linewidth=0.1,
            s=40,
            color='black',
            label='Class 1'
            )

plt.legend()
plt.title("Generated Data")
plt.show()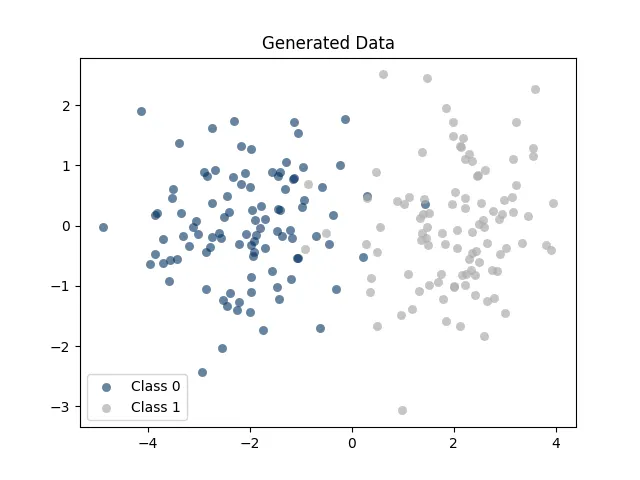

2. 建立單層感知器（Single-Layer Perceptron, SLP）

class SimpleNeuralNetwork:
    def __init__(self, input_dim):
        self.weights = tf.Variable(tf.random.normal([input_dim, 1]))
        self.bias = tf.Variable(tf.zeros([1]))

    def forward(self, x):
        return tf.matmul(x, self.weights) + self.bias 

前向傳播（Forward Propagation）

$$y = Wx + b$$

def forward(self, x):
        return tf.matmul(x, self.weights) + self.bias

forward(self, x) : 將輸入值加權及偏置，又稱為前向傳播 weights：對輸入資料的加權 bias：平移調整模型的決策邊界

3. 訓練模型階段

# 訓練模型
def train_model(model, data, labels, learning_rate=0.1, epochs=100):

	# 優化器與學習率
    optimizer = tf.optimizers.SGD(learning_rate)

    loss_history = []
    for epoch in range(epochs):
        with tf.GradientTape() as tape:
            logits = model.forward(data)  
            loss = binary_crossentropy_loss(labels, logits)

        # 計算梯度並更新權重
        gradients = tape.gradient(loss, [model.weights, model.bias])
        optimizer.apply_gradients(zip(gradients, [model.weights, model.bias]))

		# 損失函數變化紀錄
        loss_history.append(loss.numpy())
        if (epoch+1) % 10 == 0:
            print(f"Epoch {epoch+1}, Loss: {loss.numpy():.4f}")

    return model

模型超參數（Hyperparameter）

def train_model(model, data, labels, learning_rate=0.1, epochs=100)

計算梯度

with tf.GradientTape() as tape:
		logits = model.forward(data)  
		loss = binary_crossentropy_loss(labels, logits)

1. 向前傳播

使用model.forward 函數來計算data 當前的值，data 也為 x ，經函數**加權(weights)**後輸出值為 logits

2. 計算損失函數

經過binary_crossentropy_loss 來計算損失函數

損失函數是為了評估真實標籤與預測機率之間的損失值，此函數使用sigmoid函數來進行二元分類，在使用交叉熵（Cross-Entropy）來計算損失數

# 定義交叉熵損失函數
def binary_crossentropy_loss(y_true, y_pred):
    return tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=y_true, logits=y_pred))

每次訓練中的損失函數

Epoch 10, Loss: 0.1114
Epoch 20, Loss: 0.1098
Epoch 30, Loss: 0.1083
...
Epoch 80, Loss: 0.1036
Epoch 90, Loss: 0.1029
Epoch 100, Loss: 0.1024

優化器 Optimizer

主要目的是在每一次訓練中，計算梯度以及進行梯度下降，也是微積分中的微分概念，為求得最佳解。 這邊的選擇隨機梯度下降（Stochastic Gradient Descent） 的方法，並帶入學習率參數

optimizer = tf.optimizers.SGD(learning_rate)

梯度下降（Gradient Descent）

gradients = tape.gradient(loss, [model.weights, model.bias])
optimizer.apply_gradients(zip(gradients, [model.weights, model.bias]))

4. 評估模型階段

def predict(model, data) :
    logits = model.forward(data)
    return tf.sigmoid(logits).numpy() > 0.5

sigmoid函數

特性轉換成 0 或 1，適合二元分類，0.5為中間點邊界，將函數將輸入值趨近於0或1

準確率評估

計算預測函數與實際標籤的正確數與總數，並求出成功機率

def evaluate_accuracy(model, data, labels):
    predictions = predict(model, data)
    accuracy = np.mean(predictions == labels)
    print(f"Model Accuracy: {accuracy * 100:.2f}%")
    return accuracy

評估結果

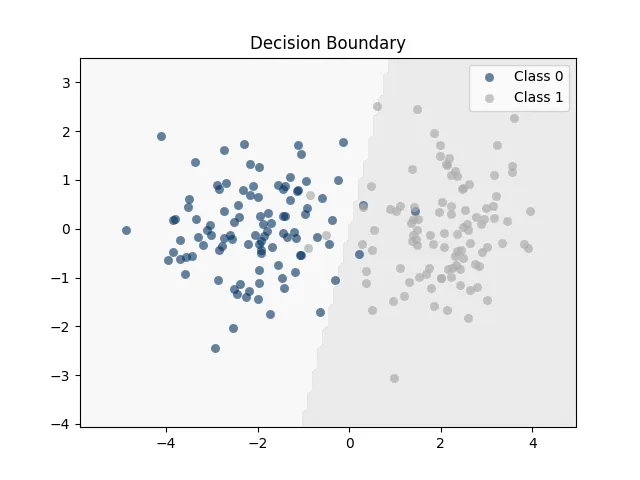
Model Accuracy: 96.50%

5. 視覺化決策邊界

# 視覺化決策邊界
def plot_decision_boundary(model, data, labels):
    x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
    y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
                         np.linspace(y_min, y_max, 100))
    grid_data = np.c_[xx.ravel(), yy.ravel()].astype(np.float32)

    # 預測網格點
    predictions = predict(model, grid_data).reshape(xx.shape)

    plt.contourf(xx, yy, predictions, cmap="binary", alpha=0.1)
    plt.scatter(data[:100, 0], data[:100, 1],
                alpha=0.7,          
                linewidth=0.1,         
                s=40,                   
                color='#003060',
                label='Class 0'
                )
    plt.scatter(data[100:, 0], data[100:, 1],
                alpha=0.3,             
                linewidth=0.1,          
                s=40,                 
                color='black',
                label='Class 1'
                )
    plt.legend()
    plt.title("Decision Boundary")
    plt.show()

6. 運行流程整合

# 訓練與測試
model = SimpleNeuralNetwork(input_dim=2)  # 建立模型
model = train_model(model, data, labels, learning_rate=0.1, epochs=100)  # 訓練模型
evaluate_accuracy(model, data, labels)  # 計算模型準確率
plot_decision_boundary(model, data, labels)  # 視覺化推理結果