線性回歸:加州房價資料集的單變量預測
環境準備
from sklearn.datasets import fetch_california_housing import pandas as pd import matplotlib import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression import numpy as np from sklearn.metrics import mean_squared_error
準備資料集
# %% 環境準備
# 設定中文字型
matplotlib.rcParams['font.family'] = 'Microsoft JhengHei' # Windows
# 載入加州房價資料集
california = fetch_california_housing()
print(california.DESCR) # 資料集的描述轉換資料格式
# %% 轉換Pandas資料格式
# 將資料集轉換為 DataFrame 和 Series 物件
# X 為特徵資料,y 為目標變數
X = pd.DataFrame(california.data, columns=california.feature_names)
y = pd.Series(california.target, name="Price")
# 資料集與目標變數的查看
print(y.describe())
X.head()平均房間數(AveRooms)特徵價格預測
選擇 AveRooms(平均房間數)作為單一特徵進行線性回歸分析
# 查看 AveRooms 特徵的分佈
print(X['AveRooms'].describe())
# 對 AveRooms 特徵評估誤差與視覺化
X_AveRooms = X[["AveRooms"]]
# 建立並訓練模型
model_uni = LinearRegression()
model_uni.fit(X_AveRooms, y)
# 預測
y_pred_uni = model_uni.predict(X_AveRooms)
# 評估誤差
mse_uni = mean_squared_error(y, y_pred_uni)
rmse_uni = np.sqrt(mse_uni)
print("評估誤差: ")
print(f"單變量模型 MSE: {mse_uni:.4f}")
print(f"單變量模型 RMSE: {rmse_uni:.4f}")資料觀察
根據 print(X['AveRooms'].describe()) 來查看特徵的分佈,在這裡我們可以注意到平均值 與 最大值
count 20640.000000
mean 5.429000
std 2.474173
min 0.846154
25% 4.440716
50% 5.229129
75% 6.052381
max 141.909091
Name: AveRooms, dtype: float64評估誤差
這裡的MSE: 1.3008 表示平均誤差來到13萬美元,根據剛剛資料平均值 與 最大值 ,發現可能是極端值造成的影響,也可能是該特徵對於房價的影響無太大的關聯,所產生的高誤差值
評估誤差:
單變量模型 MSE: 1.3008
單變量模型 RMSE: 1.1405單變量線性回歸視覺化
可以從視覺化中看到極端值對於整個數據的得影響,基於問題可能出在特徵值選擇,所以先選擇測試下一個特徵值。
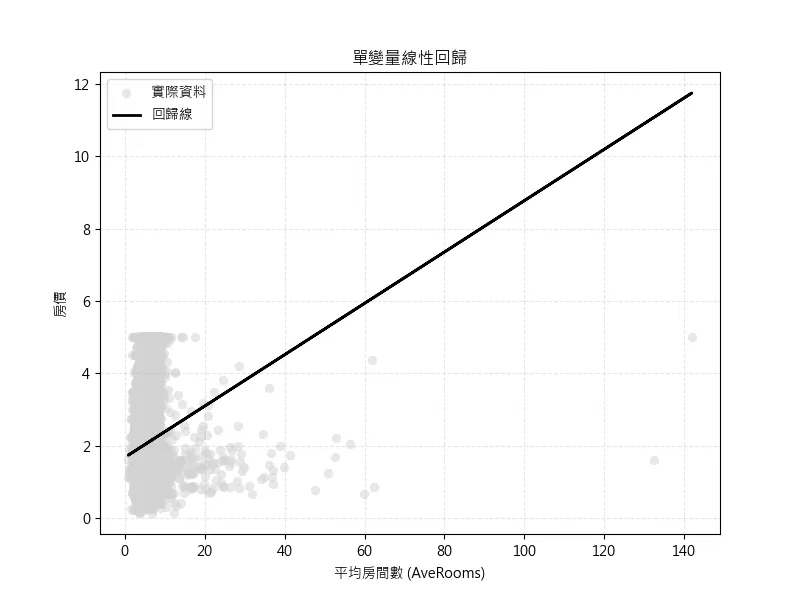
# %% AveRooms 特徵的視覺化
plt.figure(figsize=(8, 6))
plt.scatter(
X["AveRooms"], y,
color='lightgray', # 內部填色:淡灰色或其他淺色
linewidth=0.3, # 外框線條寬度
s=40, # 點的大小,預設是20,適度加大
alpha=0.5, # 透明度:讓點半透明但仍清晰
label='實際資料'
)
plt.plot(X["AveRooms"], y_pred_uni, color='black',linewidth=2, linestyle='-', label='回歸線')
# 標籤與標題
plt.xlabel("平均房間數 (AveRooms)")
plt.ylabel("房價")
plt.title("單變量線性回歸")
plt.grid(True, linestyle='--', alpha=0.3)
plt.legend()
plt.show()家庭年收入的中位數(MedInc)特徵價格預測
這是我們選擇的第二個特徵值家庭年收入的中位數(MedInc),來進行新的線性回歸模型訓練
# %% 選擇 MedInc 特徵進行單變量線性回歸
# 查看 MedInc 特徵的分佈
print(X['MedInc'].describe())
X_MedInc = X[["MedInc"]]
# 建立並訓練模型
model_uni = LinearRegression()
model_uni.fit(X_MedInc, y)
# 預測
y_pred_uni = model_uni.predict(X_MedInc)
# 評估誤差
mse_uni = mean_squared_error(y, y_pred_uni)
rmse_uni = np.sqrt(mse_uni)
print(f"單變量模型 MSE: {mse_uni:.4f}")
print(f"單變量模型 RMSE: {rmse_uni:.4f}")資料觀察
根據 print(X['AveRooms'].describe()) 來查看特徵的分佈,在這裡我們可以注意到平均值 與 最大值
count 20640.000000
mean 3.870671
std 1.899822
min 0.499900
25% 2.563400
50% 3.534800
75% 4.743250
max 15.000100
Name: MedInc, dtype: float64評估誤差
除此之外與剛剛的特徵值AveRooms 相比來說,這次的的誤差值為MSE: 0.7011 ,表示平均預測誤差價格降低至7萬美元
評估誤差:
單變量模型 MSE: 0.7011
單變量模型 RMSE: 0.8373單變量線性回歸視覺化
圖中可以觀察到,極端值對於線性回歸預測結果的影響,因此後續將使用四分位距法(IQR Method)來去除極端值。
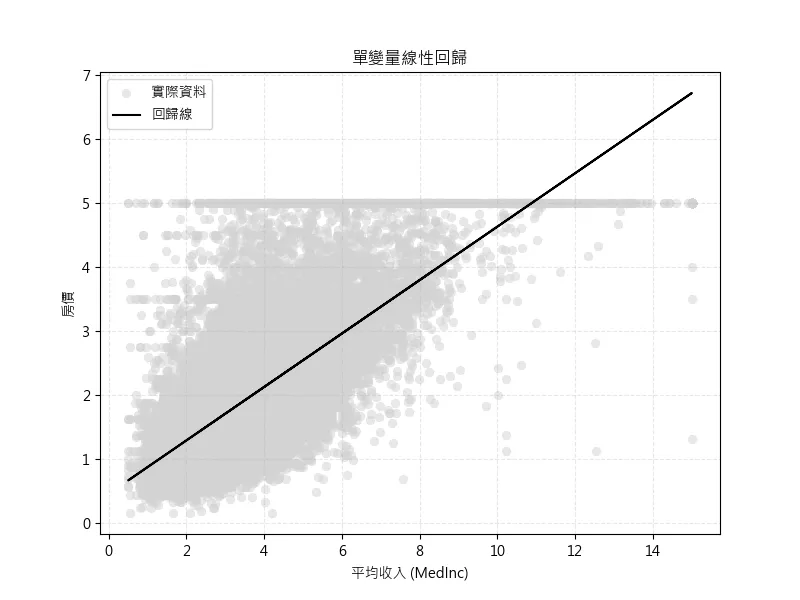
# %% MedInc 特徵的視覺化
plt.figure(figsize=(8, 6))
plt.scatter(X["MedInc"], y,
color='lightgray', # 內部填色:淡灰色或其他淺色
linewidth=0.3, # 外框線條寬度
s=40, # 點的大小,預設是20,適度加大
alpha=0.5, # 透明度:讓點半透明但仍清晰
label='實際資料'
)
plt.plot(X["MedInc"], y_pred_uni, color='black', label='回歸線')
plt.xlabel("平均收入 (MedInc)")
plt.ylabel("房價")
plt.title("單變量線性回歸")
plt.grid(True, linestyle='--', alpha=0.3)
plt.legend()
plt.show()處理異常值再次預測
為提升模型準確度,我們使用四分位距法(IQR Method)來處理 MedInc 資料中的潛在異常值。藉由過濾過大或過小的值,排除異常值對模型訓練的干擾,使預測結果更穩定與可信。
經過異常值處理後,我們重新訓練模型並視覺化新的預測結果。對比前後模型的 MSE 與 RMSE,可以評估異常值處理對模型表現的影響。
# %% 對 MedInc 特徵進行異常值處理
# 使用四分位距法(IQR Method)
Q1 = X["MedInc"].quantile(0.25)
Q3 = X["MedInc"].quantile(0.75)
IQR = Q3 - Q1
print(f"Q1: {Q1}, Q3: {Q3}, IQR: {IQR}")
# 過濾掉異常值 X
filtered_data = X[(X["MedInc"] >= (Q1 - 1.5 * IQR)) &
(X["MedInc"] <= (Q3 + 1.5 * IQR))]
# 過濾後的 y
filtered_y = y[filtered_data.index]
X_MedInc = filtered_data[["MedInc"]]
# 重新建立並訓練模型(過濾異常值版本)
model_uni = LinearRegression()
model_uni.fit(X_MedInc, filtered_y)
# 預測
y_pred_uni = model_uni.predict(X_MedInc)
# 評估誤差
mse_uni = mean_squared_error(filtered_y, y_pred_uni)
rmse_uni = np.sqrt(mse_uni)
print(f"單變量模型 MSE: {mse_uni:.4f}")
print(f"單變量模型 RMSE: {rmse_uni:.4f}")
評估誤差
這次的的誤差值為MSE: 0.6951 ,表示平均預測誤差價格降低至6.9萬美元
原本的:
單變量模型 MSE: 0.7011
單變量模型 RMSE: 0.8373
消除極端值後的評估誤差:
單變量模型 MSE: 0.6951
單變量模型 RMSE: 0.8337單變量線性回歸視覺化
從圖中可以了解,各資料分佈的位子,具有一定的線性特徵,當資料離回歸線越遠時,所預測的結果及越不準確,可能存在非線性問題。
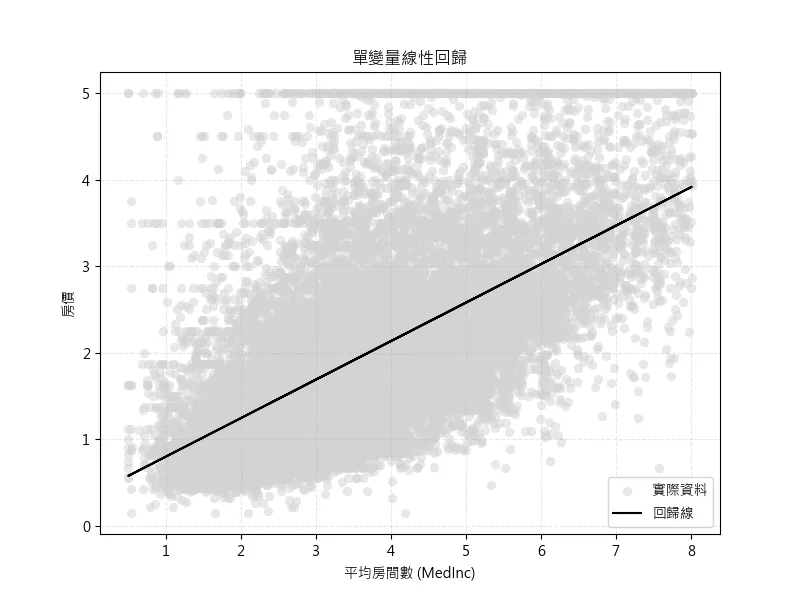
# %% 修正後的 MedInc 資料視覺化
plt.figure(figsize=(8, 6))
plt.scatter(filtered_data["MedInc"], filtered_y,
color='lightgray', # 內部填色:淡灰色或其他淺色
linewidth=0.3, # 外框線條寬度
s=40, # 點的大小,預設是20,適度加大
alpha=0.5, # 透明度:讓點半透明但仍清晰
label='實際資料'
)
plt.plot(filtered_data["MedInc"], y_pred_uni, color='black', label='回歸線')
plt.xlabel("平均房間數 (MedInc)")
plt.ylabel("房價")
plt.title("單變量線性回歸")
plt.grid(True, linestyle='--', alpha=0.3)
plt.legend()
plt.show()模型推理
最後,我們示範了如何利用訓練好的模型對單一輸入值進行房價預測。例如,若某地區 MedInc = 5.0,則模型將輸出對應的預測房價。
# %% 單一數值預測範例
example_income = pd.DataFrame({"MedInc": [5.0]})
predicted_price = model_uni.predict(example_income)
print(f"當 MedInc = 5.0 時,預測房價為: {predicted_price[0]:.4f}")當 MedInc = 5.0 時,預測房價為: 2.5787