K-Means Clustering 分群方法

簡介

K-Means 分群 (K-Means Clustering) 是一種常用的無監督學習算法，用來將資料集分成 K 個群集（群組）。該算法的目的是將資料點分成 K 個群集，使得每個群集內的資料點儘可能相似，而不同群集之間的資料點儘可能不同。這是通過最小化群集內點之間的變異（或稱為「平方誤差」）來達成的

目錄

• 學術原理
• 演算法原理
• 實作階段
• 結果分析

學術原理

此部分為記錄 K-Means 分群演算法，運行中所出現的學術原理，可以直接看到演算法原理，如果需要理解更詳細在看學術原理

畢氏定理（Pythagorean Theorem）

畢氏定理描述的是在直角三角形中，斜邊的平方，等於兩個直角邊的平方和

$$c^2 = a^2 + b^2$$

• $c$ 是斜邊的長度

• $a$ 和 $b$ 是直角邊的長度

歐幾里得距離平方的關係（Euclidean Distance）

也常稱為L2範數距離(L2 norm distance)或是歐式範數(Euclidean Norm)，都是用於求得向量空間的距離

歐幾里得距離是衡量兩點間直線向量距離的一種方式，在多維空間中，這個距離可以用畢氏定理來計算。

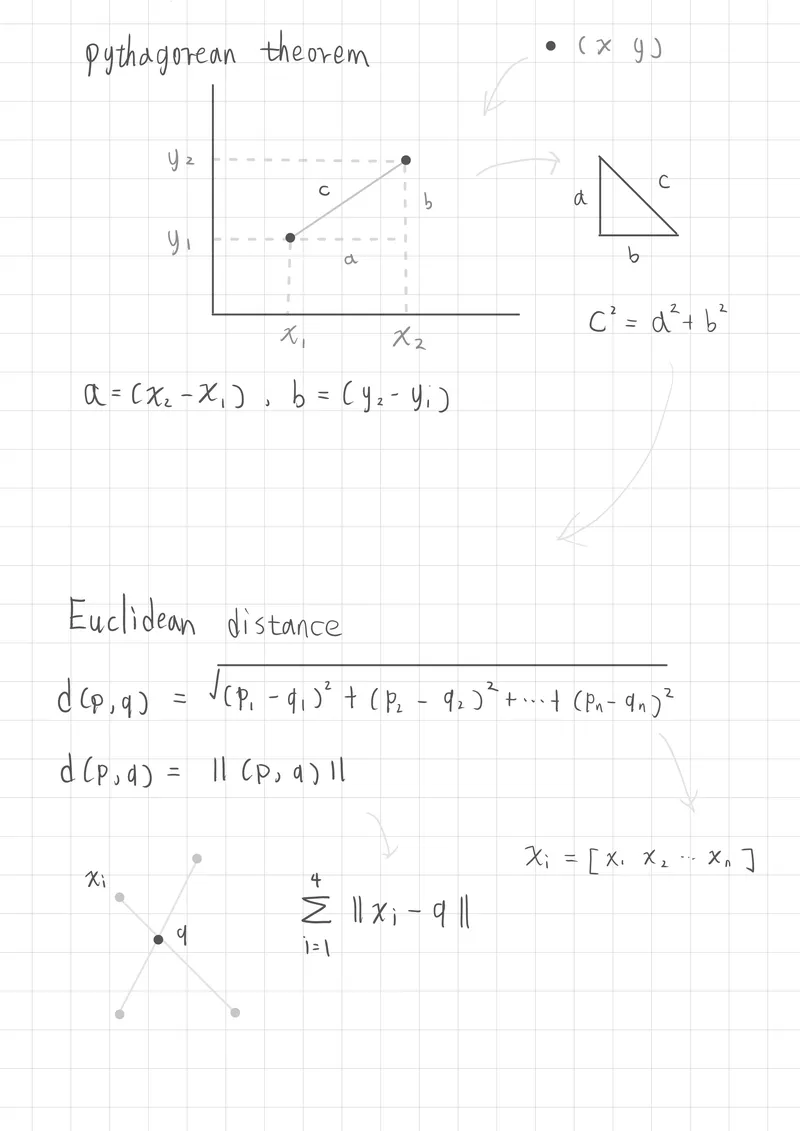
二維向量的距離關係：

假設有兩個點 $A(x_1, y_1)$ 和 $B(x_2, y_2)$，那麼它們之間的歐幾里得距離 $d$ 為： 二維向量(平面向量意味著x、y軸)

$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$

平方與根號的轉換

$$d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$$

多維度資料

當今天資料不是求得二維或三維向量距離，而是求得多維向量時候，那麼什麼是多維度向量?

可以想像多維度向量在K-mean中，他可以表示成，資料具有多個特徵，例如一筆資料可能有 [血壓、血糖、血小板、白血球] 特徵等等，此時就是多維向量的呈現

例如 (向量矩陣表示多維度資料特徵) $x = [120, 400, 500, 100, 1500, 800]$ $\mu_1​=[100,450,480,150,1400,850]$

$$(x_1 - \mu_{i1})^2 + (x_2 - \mu_{i2})^2 + \cdots + (x_n - \mu_{in})^2$$

成本函數 (Cost Function / Distortion Function)

計算單一群內的損失函數，理解很簡單，L2 泛數距離為向量距離，透過 $\sum_{i=1}^m$ 來計算每個群心內的每個點，並加總，最後透過 $\frac{1}{m}$ 計算平均數。

$$\frac{1}{m} \sum_{i=1}^m \left\| x^{(i)} - \mu_{c^{(i)}} \right\|^2$$

• $x^{(i)}$：第 $i$ 筆資料點

• $\mu_{c^{(i)}}$：$x^{(i)}$ 所屬群集 $c^{(i)}$ 的中心點

• $m$：總資料點數

總內部平方誤差（Sum of Squared Errors, SSE）

這個函數稱為 SSE，在 sklearn 框架中也稱 Inertia

K-Means 最佳化就是不斷嘗試將資料劃分為 $k$ 群，使這個 SSE 數值最小。

假設分成k群， k=3，先是計算每個群心的總向量距離，然後再加總每個群心的總向量距離

$$\sum_{i=1}^{k} \sum_{x \in C_i} \|x - \mu_i\|^2$$

• $k$：群數（number of clusters）
• $|x - \mu_i|^2$：平方歐幾里得距離（Squared Euclidean Distance)

手肘法(Elbow Method)

用來選擇 K-means 中最佳的群集數

步驟理解

1. 設定一個合理的 $K$ 範圍
2. 運行 K-means 演算法，計算每個 $K$ 對應的成本函數值
3. 透過繪製平面圖來記錄成本函數得到的數值
4. 找出變化最明顯的部分，該次數為最佳K群數

演算法原理

基本流程

1. 初始化 K 個群心（centroids）：隨機選擇 K 個點作為初始群心 可以使用肘部法則（Elbow Method）來選擇 K-means 中最佳的群集數

2. 分配資料點：將每個資料點分配到最近的群心，形成 K 個群 每一個向量都會各自計算到每一個群心的距離，並加入最近的群心

3. 更新群心：根據每個群集內的資料點，計算新的群心，即群集內所有點的均值

4. 重複步驟：直到群心不再改變（收斂），或者達到預設的最大迭代次數

實作階段

使用套件: sklearn

import pandas as pd
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA

使用資料來源 M. Cardoso. "Wholesale customers," UCI Machine Learning Repository, 2013. [Online]. Available: https://doi.org/10.24432/C5030X.

讀取資料

# 讀取資料集
df = pd.read_csv('Wholesale customers data.csv')
  
# 顯示資料概況
print("資料欄位資訊:")
print(df.info())
print("敘述統計摘要:")
print(df.describe())
print(df.head())

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 440 entries, 0 to 439
Data columns (total 8 columns):
 #   Column            Non-Null Count  Dtype
---  ------            --------------  -----
 0   Channel           440 non-null    int64
 1   Region            440 non-null    int64
 2   Fresh             440 non-null    int64
 3   Milk              440 non-null    int64
 4   Grocery           440 non-null    int64
 5   Frozen            440 non-null    int64
 6   Detergents_Paper  440 non-null    int64
 7   Delicassen        440 non-null    int64
dtypes: int64(8)
memory usage: 27.6 KB

資料處理

資料處理學術稱為特徵工程，這裡使用的是 z-score 標準化，如果原始資料接近常態分佈，大部分 z-score 值會落在 $[-3, +3]$ 區間內（99.73%）

# 移除不重要欄位，從第2欄位開始
numeric_features = df.iloc[:, 2:]

# 特徵標準化（z-score 標準化）
scaler = StandardScaler()
scaled_data = scaler.fit_transform(numeric_features)

print("第一筆資料")
print(df.head(1))
print("標準化後的資料：")
print(scaled_data[:1])  # 顯示前5筆標準化後的資料

結果

第一筆資料 Channel Region Fresh Milk Grocery Frozen Detergents_Paper Delicassen 0 2 3 12669 9656 7561 214 2674 1338 標準化後的資料： [[ 0.05293319 0.52356777 -0.04111489 -0.58936716 -0.04356873 -0.06633906]]

肘部法則（Elbow Method）

肘部法則 用來幫助選擇適合的群數 K，透過程式迴圈K+1，來找到總內部平方誤差（Inertia 或 SSE）降幅明顯變緩的位子，可以透過視覺化圖表變化來找到最佳K群數。

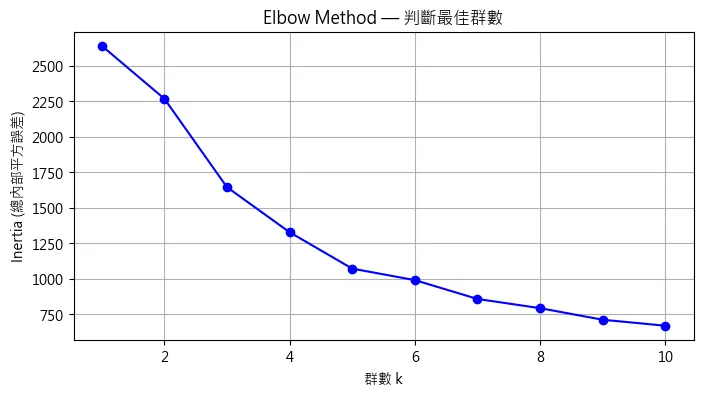
# %% 肘部法則（Elbow Method）找最佳 k 值
inertia_list = []
k_range = range(1, 11)

for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(scaled_data)
    inertia_list.append(kmeans.inertia_)

print("Inertia List:", inertia_list)
# 繪製
plt.figure(figsize=(8, 4))
plt.plot(k_range, inertia_list, 'bo-')
plt.xlabel('群數 k')
plt.ylabel('Inertia (總內部平方誤差)')
plt.title('Elbow Method — 判斷最佳群數')
plt.grid(True)
plt.show()

預測結果

# %% 預測結果
k = 3
kmeans = KMeans(n_clusters=k, random_state=42)
cluster_labels = kmeans.fit_predict(scaled_data)

# 將分群結果加入原始資料框
df['Cluster'] = cluster_labels
print("分群結果：")
print(df['Cluster'].value_counts())

• n_clusters: K群集
• random_state : 固定隨機值，避免每次測試結果不一樣

KMeans 自動執行以下流程：

• 隨機初始化 $k$ 個群心（centroids）

• 根據距離分配每筆資料到最近的群心

• 更新每個群的群心（計算平均值）

• 反覆進行直到收斂（群心不再移動，或到達預設的最大迭代次數）

PCA（主成分分析，Principal Component Analysis）

PCA是資料降維與特徵萃取的技術，這部分先不在此展開探討，只先簡單理解用途，在這裡PCA把多維資料降為至二維，以便視覺化圖表的方式表現

# %%
# PCA 將資料降為 2 維以便視覺化
pca = PCA(n_components=2)
pca_result = pca.fit_transform(scaled_data)

df['PCA1'] = pca_result[:, 0]
df['PCA2'] = pca_result[:, 1]

視覺化分群結果

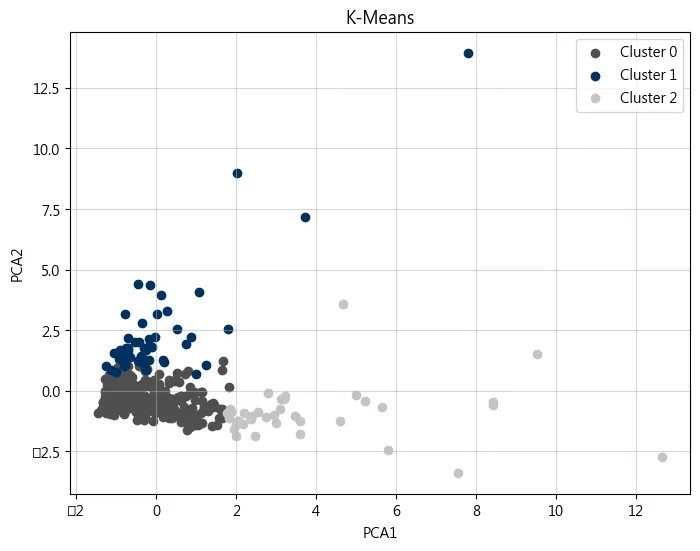
plt.figure(figsize=(8, 6))
colors = ['#4F4F4F', '#003060', '#C4C4C4']

for cluster_id in range(k):
    subset = df[df['Cluster'] == cluster_id]
    plt.scatter(subset['PCA1'], subset['PCA2'],
                label=f'Cluster {cluster_id}', color=colors[cluster_id])

plt.xlabel('PCA1')
plt.ylabel('PCA2')
plt.title('K-Means')
plt.legend()
plt.grid(True, alpha=0.5)
plt.show()

結果分析

個集群人數

分群結果：
Cluster
0    350
1     53
2     37
Name: count, dtype: int64

每個群的消費總額平均

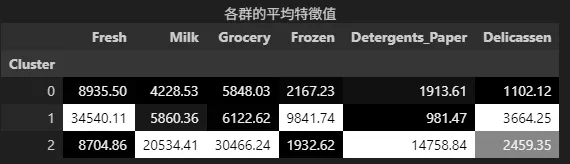
Cluster 0

整體消費總額偏低，而且群集數高達350人，且消費集中於生鮮食品，因此可能是一般消費者(家庭)

Cluster 1

整體消費總額至於中間，消費項目集中在生鮮食品、冷凍食品、熟食，可能是大型團體、零售商、小型餐飲業

Cluster 2

整體消費總額最高，消費項目集中在乳製品、日常雜貨以及清潔用品，因此可能是中、大型餐飲業者，或是商業客戶