多維向量空間中的歐幾里得距離

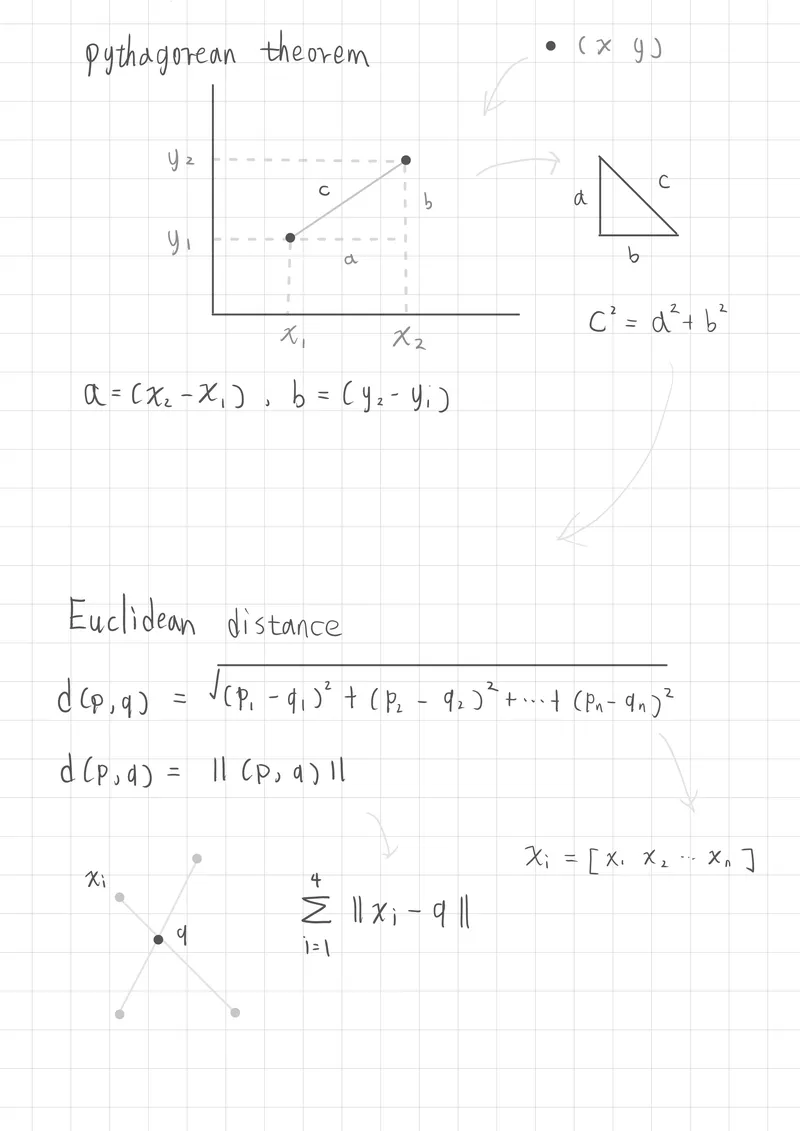
畢氏定理（Pythagorean Theorem）

畢氏定理描述的是在直角三角形中，斜邊的平方，等於兩個直角邊的平方和

$$c^2 = a^2 + b^2$$

• $c$ 是斜邊的長度

• $a$ 和 $b$ 是直角邊的長度

透過這樣的公式，我們可以知道如果一個平面座標上有兩個點，那麼我們只需要知道兩點分別的位子$(x,y)$，透過同軸相減得知距離，再透過畢氏定理公式求出$c$

歐幾里得距離平方的關係（Euclidean Distance）

在多維空間中，歐幾里得距離是衡量兩點間直線距離的一種方式，這個距離可以用畢氏定理來計算。

二維向量的距離關係：

假設有兩個點 $A(x_1, y_1)$ 和 $B(x_2, y_2)$，那麼它們之間的歐幾里得距離 $d$ 為： 二維向量(平面向量意味著x、y軸)

$$d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2$$

平方與根號的轉換:

$$d(p,q) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$$

兩個向量在空間中的距離，可以表示成 $\|p−q\|$，在k-mean聚集中就是求向量空間中心的距離

$${\displaystyle d(p,q)=\|p−q\|}$$

歐幾里得範數（L2 Norm）

$$\|x\|_2 = \sqrt{x_1^2 + x_2^2}$$

向量空間的多維度表示度

在機器學習中，資料常用多維向量表示，稱為特徵向量（Feature Vector）

$x = [120, 400, 500, 100, 1500, 800]$ $\mu_1​=[100,450,480,150,1400,850]$

而兩點之間的空間距離為

$$\|x−u_i\| = \sqrt{(x_1 - \mu_1)^2 + (x_2 - \mu_2)^2 + \cdots + (x_n - \mu_n)^2}$$

這在k-mean中很常見，因為k-mean中的點並不是指平面向量，而是一個特徵向量（feature vector），多維度的資料意味著一個點有多個特徵，所以要計算特徵向量到中心點的空間距離