神經網路的基本單元-前續

前言

在深度學習中，神經元數(Neurons)、參數數目(Parameters)是理解模型結構重要指標

神經元(Neurons)

神經元指的是神經網路中的基本單位，負責接收前一層的輸入，所以每一個神經元會具備同樣的輸入，但是不同神經元會有不同的反應，取決於他們之間的關聯。

日常的例子

當你看到狗，你的大腦可能會有一大部分的神經元受到激活，每一個神經元都會依據不同的特徵進行反應。

數學矩陣

從數學矩陣來看，每一層的輸入可以視為矩陣張量

假設資料維度是二維張量(Tensor)，即輸入為 $m \times n$ 矩陣

• $m$ 是樣本數

• $n$ 是特徵數

每個神經元會對應到這些特徵，並計算加權總和，從矩陣乘法規則中，也可以明白神經元的傳遞原理

例如，為何可以從3個神經元中傳遞至5個神經元，最終結果又收斂回1個神經元

參數(Parameters)

指神經網路中所有的權重（Weights）和偏置（Bias）的總和。這些參數會隨著訓練過程被不斷調整，參數數目直接影響模型的容量與計算負擔，通常參數越多，意味著模型模型越大也越複雜。

日常的例子

繼續剛剛貼近日常的例子，假設你看到狗，你的大腦大部分神經元都一同受到刺激，但是你所知道的資訊細節不一定豐富，例如你不只是辨識出這是一隻狗，同時你也觀察到他在搖尾巴，聯想到他開心等等，這些後續聯想到的細節，可以理解成參數。

前向傳播（Forward Propagation )

透過前向傳波的原理可以更好的理解神經元與參數的關係，這部分涉及矩陣數學中的乘法原理

公式表達:

$$y = f(W X + b)$$

• $y$ 是神經元的輸出（對應一個神經元）

• $W$ 和 $b$ 是參數（權重和偏差）

• $x$ 是輸入向量（可能是上一層多個神經元的輸出）

• $f$ 是激活函數

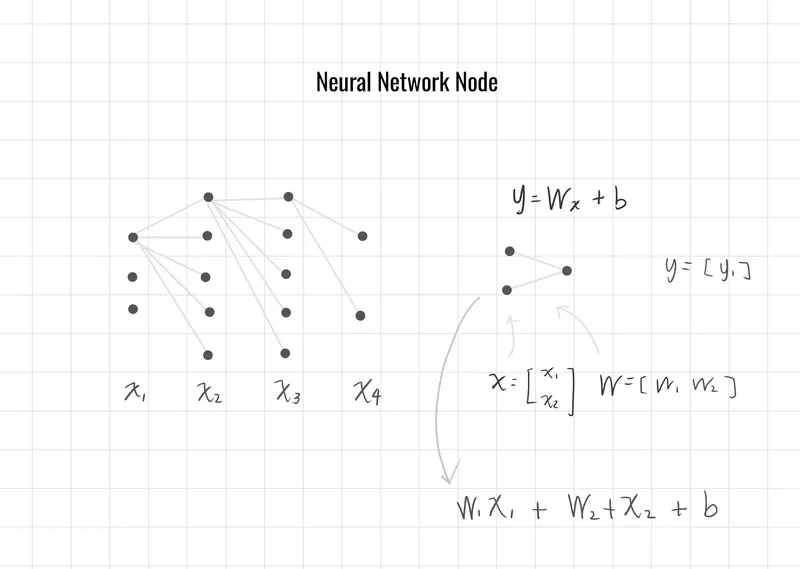
計算方法

以一個神經網路(Neural Network)為例子，如下圖