r036_logo

有限馬可夫決策過程（Finite Markov Decision Process, Finite MDP）

馬可夫決策過程是強化學習中的架構，特點是未來的狀態只取決於當前狀態與動作，與過去無關，在這個狀態性質下則稱為馬可夫性質（Markov Property）。

基礎元素有：

(S,A,P,R,γ)(S, A, P, R, \gamma)
  • SS：有限的狀態空間（State space）
  • AA：有限的動作空間（Action space）
  • PP：轉移機率函數（Transition probability），表示在狀態執行動作轉移到狀態的機率
  • RR：報酬函數（Reward function），在狀態採取動作後所得到的期望報酬
  • γ∈[0,1]\gamma \in [0,1]：折扣因子（Discount factor），用來折扣未來的報酬，當考慮長遠報酬則趨近1，短期報酬則越小

決策流程

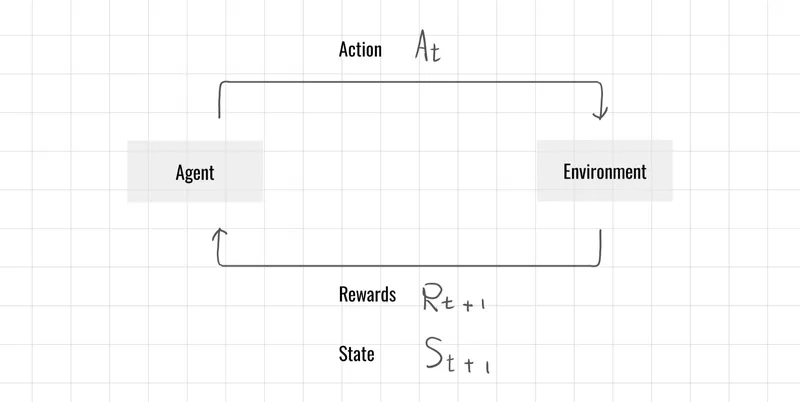什麼是強化學習 在有限馬可夫決策過程中，智能體（Agent）與環境（Environment）在離散時間點進行互動。於每個時間步 tt，智能體觀察當前環境狀態 StS_t，並基於該狀態選擇動作 AtA_t。環境接收此動作後，會回應一個數值獎勵 Rt+1R_{t+1} 以及下一個狀態 St+1S_{t+1}，促成智能體與環境之間的連續交互過程。

離散時間（discrete time）表示為：

t=0,1,2,3,…t = 0, 1, 2, 3, \ldots

在強化學習中，智能體與環境的互動即發生於這些離散的時間步數（time steps），每一步對應一次觀察、行動與回饋。

將整體互動過程用橫式表示則為：

(S0,A0,R1,S1,A1,R2,S2,A2,R3,…)(S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, \ldots)

轉移機率函數（Transition Probability）

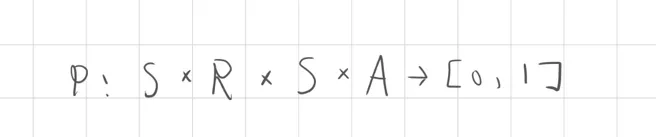
轉移機率函數也稱為動態函數，這裡以P表示，包含狀態S、獎勵R、動作A狀態集合，在同一次行動中的機率將映射在0到1之間。 什麼是強化學習

動態函數

馬可夫性質下的動態函數表達為下一狀態與獎勵只依賴當前狀態與動作，而這個動態函數的轉移機率則可以表示為以下

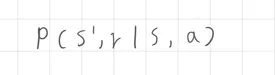
什麼是強化學習

該公式表示在當前狀態 ss 執行動作 aa，並且轉移到下一個單一狀態 s′s' 的機率，獲得獎勵 rr 的機率

機率分布(probability distribution)

理解動態函數的轉移機率後，再來是延伸機率論中的機率分布的表示方法

聯合機率方法表示為:

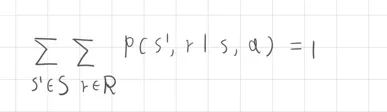
什麼是強化學習

該公式表示為當滿足(s,a)狀態動作下，轉移至下一個動作所獲得的獎勵機率總和為1，需要留意這裡的(s,a)是以發生單一事件，而轉移至下一個可能發生的所有狀態與獎勵，因此將所有的事件機率加總機率將等於1。

邊際機率

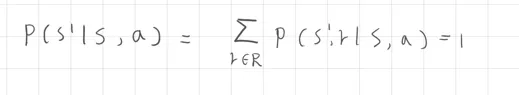
邊際機率與聯合機率不同，這部分不考慮所有的狀態s'，只考慮一個狀態下的所有獎勵機率，因此這裡將所有可能的獎勵值 rr 的機率加總起來，而機率總和等於1 什麼是強化學習

期望獎勵 (Expected Reward)

簡單回顧一下期望值的核心，期望值為一個連續事件機率下的獎勵平均值，表示為

期望值=獎勵×機率\text{期望值} = \text{獎勵} \times \text{機率}

在有限馬可夫決策過程中，若考慮不同條件下的參數，則期望獎勵表示為

1. 二個參數 (two-argument)

若計算當前r(s,a)r(s,a)狀態、動作對未來的獎勵期望值表示為

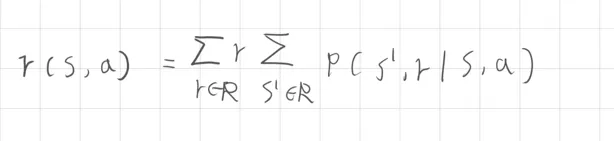
什麼是強化學習

在狀態 ss 採取動作 aa 時，對所有可能的 s′s' 和 rr 做加權平均，求得期望值

一個例子

假設

  • R={r1}R = \{r_1\}，且 r1=1r_1 = 1
  • S={s1,s2}S = \{s_1,s_2\}
  • p(s1,r1∣s,a)=0.3p(s_1, r_1 \mid s,a) = 0.3
  • p(s2,r1∣s,a)=0.2p(s_2, r_1 \mid s,a) = 0.2
1×0.3+0.2=0.51 \times 0.3+0.2=0.5

2. 三個參數 (three-argument)

當已知下一狀態 s′s' 時，我們只考慮這個狀態下的情況，則為 r(s,a,s′)r(s,a,s') ，該獎勵期望值表示為

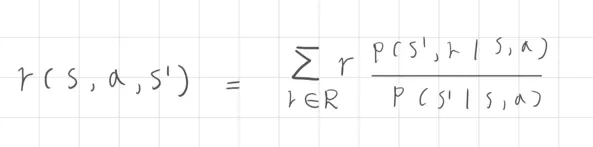
這裡應用的是加權總合的概念，由於已知狀態s′s'因此只考慮該狀態s′s'的rr獎勵參數進行加總 什麼是強化學習

分母 是轉移到 s′s' 的機率總和 分子 是到達 s′s' 並獲得不同獎勵的加權後的總和

一個例子

假設

  • S={s1,s2}S = \{s_1, s_2\}
  • R={1,2}R = \{1, 2\}
  • p(s1,1∣s,a)=0.3p(s_1, 1 \mid s, a) = 0.3
  • p(s1,2∣s,a)=0.2p(s_1, 2 \mid s, a) = 0.2

分母是s'狀態轉移機率

p(s1∣s,a)=0.3+0.2=0.5p(s_1 \mid s,a) = 0.3 + 0.2 = 0.5

計算 s1s1 的獎勵期望值

r(s,a,s1)=1⋅0.3+2⋅0.20.5=0.3+0.40.5=0.70.5=1.4r(s,a,s_1) = \frac{1 \cdot 0.3 + 2 \cdot 0.2}{0.5} = \frac{0.3 + 0.4}{0.5} = \frac{0.7}{0.5} = 1.4