MDP回報獎勵定義在持續任務與情境任務中的表示

折扣因子 (Discount Factor, $\gamma$)

$\gamma$ 折扣因子

$0 \leq \gamma \leq 1$

• $\gamma$ 小 → 著重即時獎勵（短期目標）
• $\gamma$ 大 → 重視未來獎勵（長期目標）

回報 (Return)

回報 (Return) 被定義為獎勵序列，指的是從時間步 $t$ 開始，往後累積獲得的獎勵總和

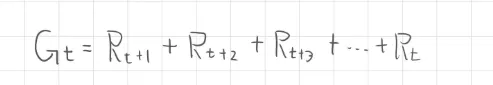
連續任務

在許多環境下，強化學習的代理並不會區分回合數，而是持續的不斷進行，稱為連續任務，這是一個無窮加總的過程，因此回報的定義在這個情境是不允許的，因為這意味著回報無限大且收斂。

因此連續任務過程中則與$\gamma$ 折扣因子有關，基於前面所提到折扣因子的參數區間，這意味著這個無窮的過程最終能被收斂，使得每個未來獎勵被乘上係數而衰減

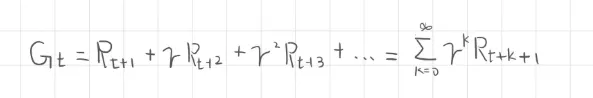
例如折扣因子為 $\gamma^0 = 1 ,\gamma^1 = 0.9 ,\gamma^2 = 0.81$ 則表示當下的獎勵沒有折扣，而延後步數越往後折扣則越來越少最終收斂

遞迴的演算法形式

為了清楚理解回報的性質，這裡回報展示了離散、無窮級數、遞迴過程，如果 $T$ 為停止時間，而 $t$ 為當前時間，即使是連續任務，我們也可以定義回合將於第 $t+1 = T$ 回合數 $G_T = 0$

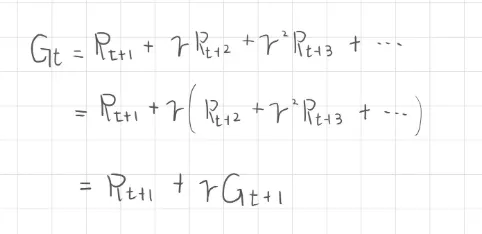
另外，這也表達了馬可夫性質（Markov property） ，將一個長期問題轉換成當前獎勵 $R_t + 1$與未來回報 $G_t+1$ ，這種形式也是 動態規劃 (dynamic programming) 的基礎概念

情境任務與持續任務的統一表示

回顧剛剛所提到的持續任務仍可以是有限的方法，稱為吸收狀態( absorbing state )，簡單表示則為 $+1 , +1 , +1, 0, 0, 0,...$

情境任務與持續任務的統一表示意義在於使數學公式一致性，不需將有限的情境任務(Episodic Task) 與 無限的持續任務(Continuing Task) 分開定義，以及在程式實作與動態規劃上也更清楚的定義了回合步數

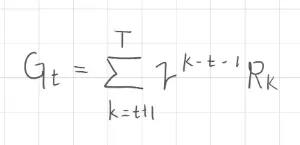
T 可以是有限或無限

t 為回報計算的起始時間

這裡的 $k = t + 1$ 中的 +1 可以理解成避免程式從 $0$ 開始數的迴圈定義，$k$ 是實際的時間

而 $\gamma^{k-t-1}$ 這裡的 -1 則是為了對齊指數的延後計算的特性使，前面 持續任務 有提到。