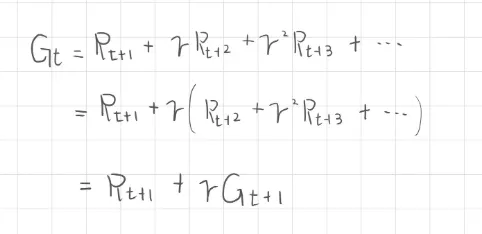貝爾曼方程中的價值函數

前續

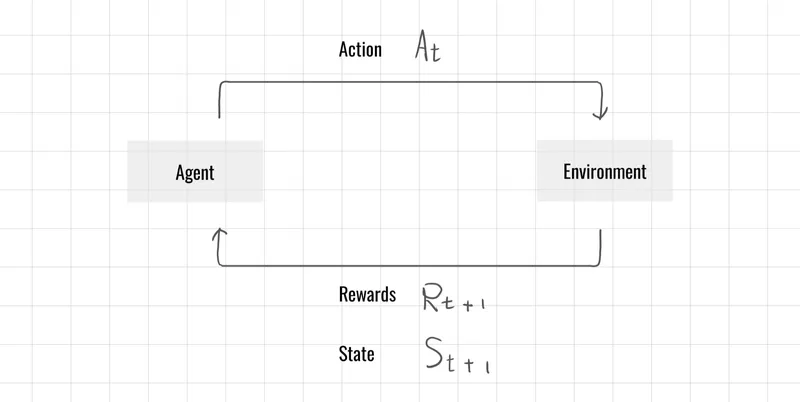
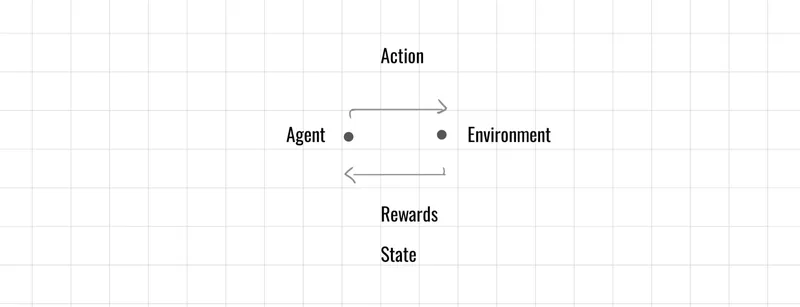
在討論價值函數之前，需要先理解獎勵期望值與回報的觀念，此篇將介紹策略(Policy) $\pi$ ，在先前我們所討論的馬可夫決策過程中，只討論了在有限或是無限回合上獎勵總和的觀念，

而本篇討論的則是更具體的推導過程，從價值函數在到貝爾曼方程，貝爾曼方程不是直接給出最佳策略，而是用來評估最佳策略的價值，這些觀念攸關了強化學習在動態規劃上的基礎

策略 (Policy)

策略是指在給定狀態下，代理選擇各種可能動作的機率分佈

$$\pi(a \mid s) = P[A_t = a \mid S_t = s]$$

$s$ 為當前狀態

$a$ 為可能採取的動作

$\pi(a \mid s)$ 表示在狀態 $s$ 下選擇動作 $a$ 的概率

策略 $\pi$ 定義了在每個狀態下採取各種行動的機率分佈 $\pi(a|s)$，有了策略我們便能在價值函數的評估中去評估，在狀態下的每一個動作所能帶來的獎勵。

狀態價值函數 (State Value Function)

價值函數 (Value Function) 是一種對未來期望回報評估，狀態價值函數只考慮一個狀態 S ，在這個狀態下的所有策略動作機率分佈，並將所有動做未來累積的獎勵加權總

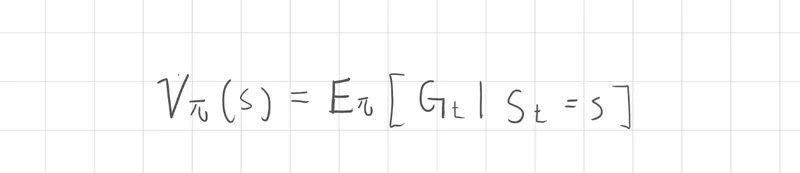
公式表示當處於狀態 s 中，所能獲得的價值評估，這裡延續了回報G的概念，因此它決定了未來的狀態轉移與回報序列，而這正是價值函數的概念

這裡所提到的回報概念在我們上一篇文章中有介紹，如果不熟悉可以參考 https://r036.blog/articles/reinforcement-learning/RL20250003

不管是回報還是價值函數屬於抽象定義，而貝爾曼方程中的概念可以得知更具體的描述

行動價值函數 (Action Value Function)

另一個情況則是行動價值函數則是同時考慮了狀態 S 與 動作 A ，也就是在特定狀態下採取某個動作後所得到的期望價值

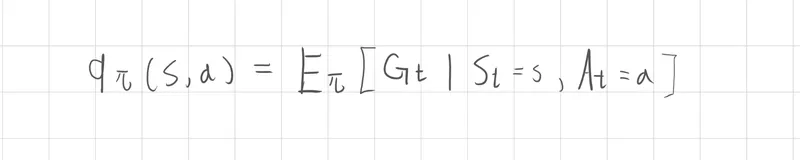
貝爾曼方程的價值函數定義

貝爾曼方程（Bellman Equation） 是來理解與計算最佳策略下各個狀態價值的方法，它透過遞迴的概念，將問題分解成即時獎勵與未來回報價值。透過這種方式，我們可以逐步評估每個狀態的重要性，並最終找出在整個環境中表現最好的行動策略。

貝爾曼方程

價值函數中的期望值包含了回報G與狀態，回報G的展開我們得到了當下的即時獎勵R，以及帶有折扣的回報G，這部分我們已經在馬可夫決策過程介紹過。

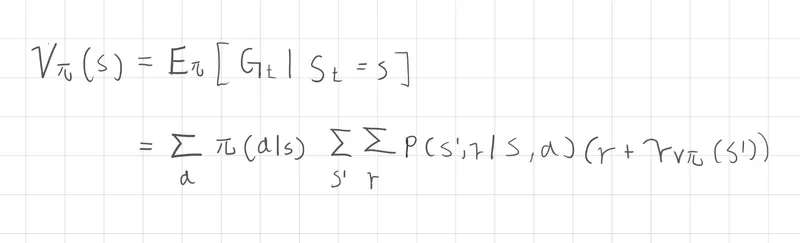
繼續將價值函數的期望值的表達式展開

1. 我們需要先計算策略中每個動作的機率

2. 根據環境的不確定性轉移到未來狀態 s' 並獲得 r 的機率

3. 將狀態轉移的機率乘上即時回報 r + 折扣後未來的價值

你可以發現貝爾曼方程本質上是更詳細的描述了策略動作機率、期望值算法、狀態轉移機率、回報獎勵，這些觀念與馬可夫決策過程提到的概念是一樣的。

結語

此篇我花了不少時間消化，結論是貝爾曼方程的定義敘述上比較複雜，然而在理解上只需要拆解每一個小部分，此章節我們可以簡單構思少量的動作 a 或是 狀態 s ，但是當這些集合參數是數以千計的時候，工程師或是電腦科學家只需要構思開發架構，剩下的則是計算機最擅長的事情，因為強化學習本質還是給計算機運行的。

如果在解讀上還是有些吃力，可以將每個部份的觀念拆解，回顧馬可夫決策過程的核心觀念，需理解無窮的數學觀念、或是在程式碼運行的遞迴觀念、機率論、統計學等等，最後才到應用層面所面對的子領域知識。