資料科學基礎-2：探索性資料分析 (Exploratory Data Analysis)

探索性資料分析 (Exploratory Data Analysis)？

EDA 的主要目的是幫助在做出任何分析之前，先查看與了解數據。它可以幫助識別明顯的錯誤，以及更好地理解資料中的規律特性，檢測異常值或異常事件，找到變數之間的有趣關係 [1]。

目標:

  • 理解資料的結構與特性
  • 找出資料中的模式、趨勢與異常
  • 進行後續的機器學習應用

環境套件

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

matplotlib

matplotlib圖表資料將自動擷取pandas.DataFrame 物件

columns = ["sepal_length", "sepal_width", "petal_length", "petal_width", "class"]
df = pd.read_csv("../Dataset/iris/iris.data", header=None, names=columns)
print("Pandas DataFrame 物件型態", type(df))

直方圖 (Histogram)

顯示一個數值特徵的分佈情形

使用Iris dataset 針對四種特徵值的分佈狀態，以視覺化方式呈現。

# 每個特徵的直方圖
df[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']].hist(bins=20, figsize=(10, 8))
plt.tight_layout()
plt.show()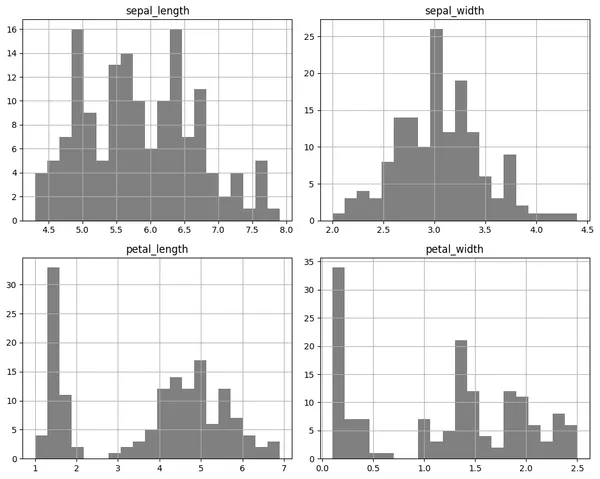

iris_Histogram

直方圖特性:

  • 是否呈現常態分佈（鐘型）
  • 是否有偏態（左偏、右偏）
  • 數值範圍

數據分析

從直方圖可以看到萼片長度(sepal_length)呈現一個常態分佈，且在發現三種較多的分布區間，分別是5.0、5.5、6.2 。

萼片寬度(sepal_width)呈現一個常態分佈，且在 3.0 呈現最多數

花瓣長度(petal_length)在 1.5 區間呈現最多數，且在 3 ~ 7 之間呈現一個常態分佈。

花瓣寬度(petal_width)與長度呈現狀態類似，在 0.1 呈現最多數，且其他多集中在在1.3、1.8、2.2 。

箱型圖（Box Plot）

視覺化每個特徵的數據分佈範圍和異常值。

# 每個特徵的箱型圖
plt.figure(figsize=(10, 8))
sns.boxplot(data=df[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']])
plt.show()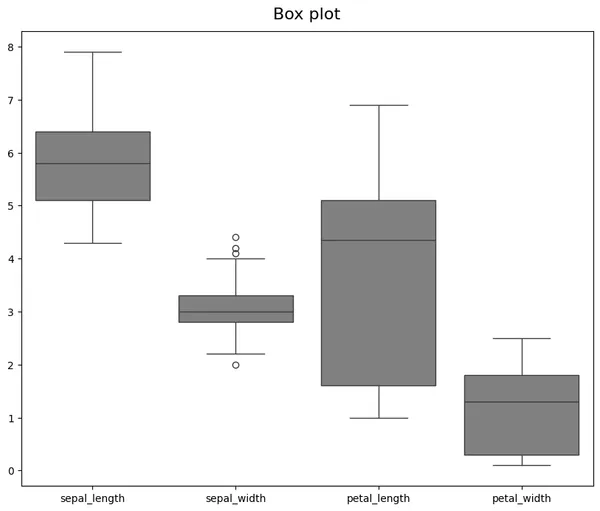

iris_BoxPlot

特性:

  • 最小值（Minimum）

    資料中最小且未被視為離群值的數值。

  • 最大值（Maximum）

    資料中最大且未被視為離群值的數值。

  • 中位數（Median / Q2）

    將資料一分為二的中心點，表示 50% 的資料比它小。

  • 下四分位數（Q1 / First Quartile）

    表示 25% 的資料比它小。

  • 上四分位數（Q3 / Third Quartile）

    表示 75% 的資料比它小。

  • 四分位間距（IQR, Interquartile Range）

    定義為 Q3 - Q1，代表中間 50% 資料的範圍。

  • 離群值（Outliers）

    若數值：

    • 小於 Q1 - 1.5 × IQR 下鬍鬚（Lower Whisker）
    • 或大於 Q3 + 1.5 × IQR 上鬍鬚（Upper Whisker）

    則會被視為離群點，以獨立的「點」顯示在圖外。

數據分析

在萼片寬度(sepal_width)中發現四個離群值（Outliers），三個離群值在上鬍鬚（Upper Whisker），一個離群值在下鬍鬚（Lower Whisker）

特徵對關係圖(Pairplot)

同時顯示多個特徵之間的雙變量關係

# 配對圖，視覺化特徵間的關係
sns.pairplot(df, hue="class", diag_kind="hist")
plt.show()

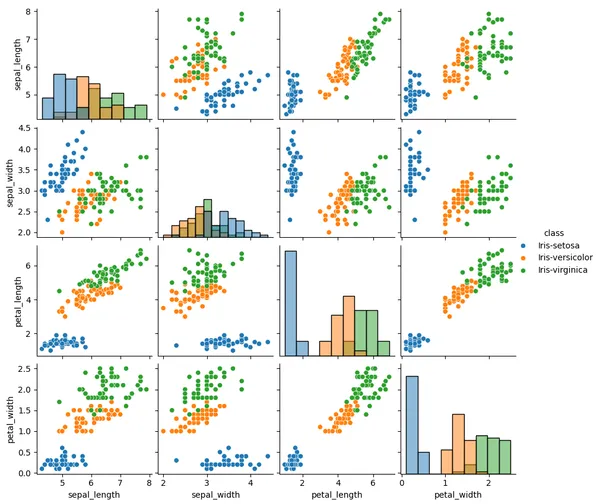
iris_Pairplot

特性:

  • 特徵間的相關性、線性關係
  • 各物種（class）的分群情況
  • 哪些特徵可用來區分不同類別

數據分析

從特徵對關係圖(Pairplot)表明，萼片寬度(sepal_width)與花瓣寬度(petal_width)的關聯中，對於不同品種的鳶尾花中呈現「明顯分隔」的情況，並且對比上述的箱型圖可以發現，萼片寬度(sepal_width)的離群點三個>4 的值，在這邊呈現在藍色類別標籤，也就是 iris-setosa 品種，可以從這樣的離群值中，判斷這個品種是否存在某種異常特點。

相關矩陣熱圖 (Correlation Matrix Heat map)

使用顏色來表示變數間的相關性強度(strong correlation)，顯示強正相關(strong positive correlation)與強負相關(strong negative correlation)，能夠迅速理解哪些特徵之間的關係。

# 相關矩陣
correlation = df[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']].corr()
plt.figure(figsize=(8, 6))
sns.heatmap(correlation, annot=True, cmap="coolwarm", fmt=".2f")
plt.show()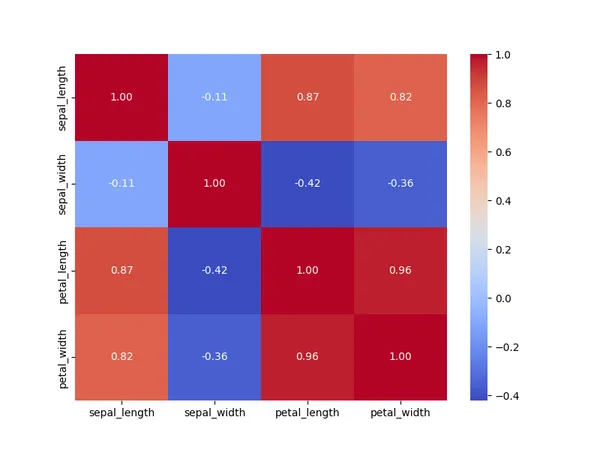

iris_CorrelationMatrixHeatmap

特性:

  • +1 表示完全正相關：當一個變數增加時，另一個變數也會隨之增加。
  • 1 表示完全負相關：當一個變數增加時，另一個變數會減少。
  • 0 表示無相關：兩個變數之間沒有線性關係。

數據分析

相關矩陣熱圖中表明，花瓣寬度(petal_width)與花瓣長度(petal_length)呈現強正相關高達0.96 ，這表明花瓣長寬的關聯性是非常明顯的正成長。

相比之下，萼片(sepal)長寬與花瓣(peta)長寬卻呈現 -0.42、-0.36 的負相關，這表明兩者間存在較低的負向關聯。

根據相關矩陣熱圖，觀察到鳶尾花的花瓣與萼片存在許多線性關聯，其中有些為顯著的正相關，而有些顯示為弱的負相關。

參考文獻

[1] What Is Exploratory Data Analysis (EDA)? (n.d.). IBM. https://www.ibm.com/think/topics/exploratory-data-analysis