【論文概念】Long-term forecasting of hourly retail customer flow on intermittent time series with multiple seasonality

版權與使用聲明

此文章主要目的為學術概念、方法紀錄，以及心得觀點。
本文將遵守著作權法，依合理使用原則（如學術引用、評論等目的）撰寫。
如有引用圖片，均依原始授權條款（如 Creative Commons、Open access）使用。
如需完整研究細節、圖表與原始內容，請參考原始論文出處。

論文出處

Martim Sousa, Ana Maria Tomé, José Moreira, Long-term forecasting of hourly retail customer flow on intermittent time series with multiple seasonality, Data Science and Management, Volume 5, Issue 3, 2022, Pages 137-148, ISSN 2666-7649, https://doi.org/10.1016/j.dsm.2022.07.002

導讀摘要與結論

此篇研究主軸為預測每個時間點零售客戶的數量，這關於了時間序列(time series)與季節週期性的關係，而這些概念適用於任意時間序列有關的資料，文中提到的多步預測策略則介紹資料的運作方式，使的在深度學習模型的訓練上有更多的開發方向。

而本文所提出的加權平均集成模型（Weighted Average Ensemble, WAE）是整個論文的核心，文中描述了WAE的架構，從流程最初資料處理至預測模型(Forecasting Models)，在到評估指標、篩選、加權，最終集成為WAE預測模型，在後續測試結果中展示WAE模型優於本文所使用的各個預測模型。

介紹

人力優化（Workforce optimization）是一個活躍的研究主題，因為它能為企業帶來不可忽視的人事成本降低

另一個需要克服的問題是，如何應對所謂的multiple seasonality問題，並讓機器學習模型有效學習到時間週期所發生的特徵變化

這些研究不僅是應用在一般的人力優化上，也可以應用至各個商業行為分析，以及具有季節週期性的資料預測

目的

截至2022年，文獻回顧顯示，尚無論文探討多步預測情境下，具有多重季節性週期的間歇性時間序列，這導致模型選擇上的誤導性結論，因此，該研究針對此問題提出相應之解決方案

該研究主要目標是能準確預測長達一個月的零售商店顧客流(time series of customer entries)，以幫助企業做出良好的決策

貢獻

該研究有幾項貢獻：
(1) 季節性遞迴法（seasonal recursive）大幅優於其競爭者遞迴策略（recursive strategy）

(2) 線上季節性 z 分數異常值檢測（online seasonal zscore outlier detection）明確偵測出大量異常值，減少餵給模型的噪音，進而降低預測誤差；

(3) 多重季節性簡單法（multiple seasonal naïve）表現優於任何單一季節性簡單法。

(4) 提出加權絕對誤差框架（WAE framework, Weighted Absolute Error），他的表現在該研究中勝過所有模型。

多重季節性

什麼是多重季節性問題，多重季節性指的是在同樣的時間週期，將出現類似的行為模式

舉個例子

在每日季節性中，觀察出早上或傍晚高峰值

在月季節中，觀察出月中或月底，原因是發薪日或其他因素的影響

在年季節中，觀察是否在不同節慶或是季節發生變化

單位以一個小時的時間序列來表示每日、每周、每月和每年，並稱為Seasonal cycle length，季節時常大小設定為24的倍數，即24、168、672和8736

資料集與前處理

資料集

該資料集包含 98 條實際零售時間序列，涵蓋的資訊時間範圍為 2015 年 1 月至 2019 年 11 月。

而 2019 年 11 月的資料被用作驗證集（validation set）進行模型評估，其餘年份的資料則用於訓練模型。

資料具有以下特性：

• 資料不連續（由於非營業時段造成的缺失）

• 多重季節性問題（日、週、月、年）

• 長期預測需求（例如：預測未來 720 小時，即 30 天）

演算法 — 線上季節性 z 分數異常值檢測（Online seasonal zscore outlier detection）

該研究提出一種演算法：線上季節性 z-score 異常值檢測（Online seasonal zscore outlier detection）

這些異常值可能出現在特殊事件、國定假日、資料錯誤等等，在樣本數據不夠多或是資料不夠穩定時，該研究建議以保留整體趨勢為優先。

演算法將透過z-score找出極端值，並替換為相同季節值的平均數，使模型在訓練時不受到異常值的影響，而降低了整體趨勢的預測準確度

演算法的重點整理

最開始: 輸入時間序列資料陣列，以及季節元素的總週期數 $k$ ，以及季節循環長度 $s$

第3行: while 迴圈表示處理逐筆資料

第6行: while 迴圈負責找出目前時間序相對應的季節時間

第9行: 負責判斷該時間資料是否為極端值，原理就是計算出z-score，並且將上界和下界去加入倒O集合內，而這個z-score的平均數與標準差則是以相同季節資料為基準參數。

z-score

z-score 是統計學（Statistics）中用來衡量一個資料點與整體資料平均值的距離，並以標準差（Standard Deviation）為單位的指標

在本演算法中，計算 Z-score 所使用的平均值與標準差，僅基於相同季節位置的歷史資料，而不是全體資料。

異常資料填充

當我們擁有了擁有異常值的O集合，則將每一個異常值，以相同季節總平均值替代。

$k$ 是前幾個季節元素的數量，$s$ 是季節循環長度，透過函數加總，最後再取平均值來代替

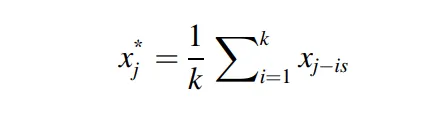
MinMax 標準化 (MinMax Normalization)

MinMax 標準化為機器學習常用的標準化方法，因為它確保了更穩定和更快速的收斂，讓模型更容易進行訓練

它會將每個元素映射到區間 $[0, 1]$，計算公式如下：

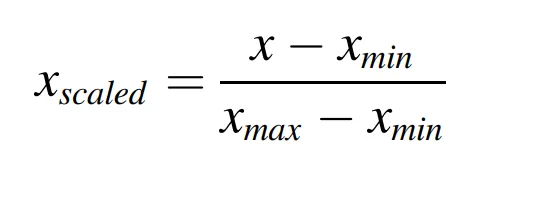
方法

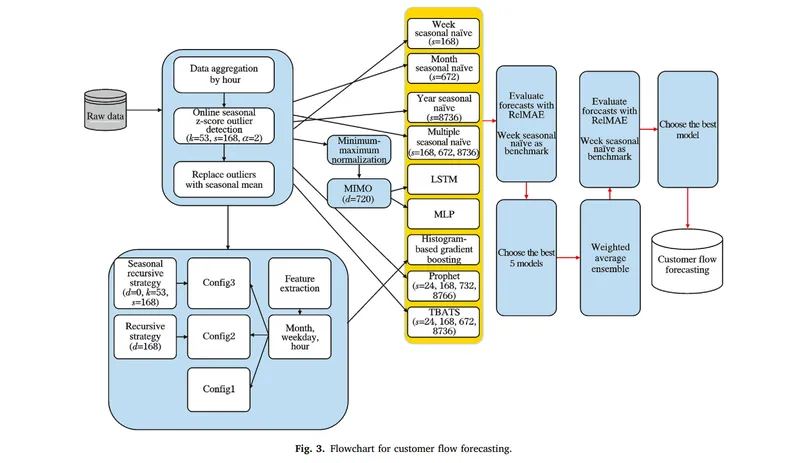
主要的流程架構，

最一開始進行資料前處理，包括線上季節性 z-score 異常值檢測（Online Seasonal Z-score Outlier Detection）與MinMax 正規化（MinMax Normalization）

再來透過多步季節性策略（multistep seasonal strategies）重新組織時間序列資料，並輸入至各種預測模型進行訓練

訓練完成後，透過相對平均絕對誤差（Relative Mean Absolute Error, RelMAE）評估模型效能，選出誤差最小的前五名模型

這些模型會使用加權絕對誤差法（Weighted Absolute Error, WAE）進行組合，並再次使用 RelMAE 評估整體效能，最終選出表現最好的模型作為最終預測結果。

模型

該研究中使用的幾個現有模型，在流程圖中的黃色區塊標示

季節性天真方法（Seasonal naïve）

季節性天真方法（Seasonal naïve）是一種針對季節性時間序列的簡單預測方法，該研究中，預測值設定為，等於最後一次觀察到的相同期季節的值。

儘管此方法較為簡單，卻能勝過更複雜的方法，特別是在高度季節性且無明顯趨勢的時間序列中。

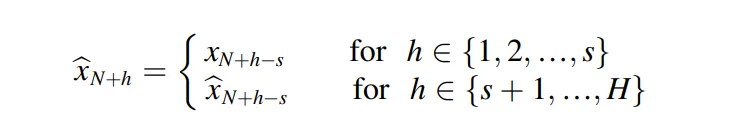
多重季節性天真方法 (Multiple seasonal naïve)

該研究將季節性簡單法延伸至多重季節性，透過對不同季節週期長度多次套用季節性簡單法，並對各預測結果取平均值來達成。

HistGB（Histogram-based Gradient Boosting）

基於分桶優化的梯度提升決策樹模型，能高效處理結構化資料的回歸與分類任務，適合配合特徵工程應用於時間序列預測。

MLP（Multi-Layer Perceptron）

經典的前饋式神經網路，透過多層非線性轉換學習輸入與目標之間的複雜函數關係，適用於固定長度的向量輸入資料。

LSTM（Long Short-Term Memory）

一種具備時間記憶能力的遞迴式神經網路，可捕捉長期與短期依賴，廣泛應用於時間序列與序列資料建模。

Prophet

由 Meta（Facebook）開發的可解釋時間序列預測模型，結合趨勢、週期與節日效應，適用於具有明確結構的業務預測場景。

TBATS（Trigonometric, Box-Cox, ARMA, Trend, Seasonality）

一種專為處理多重季節性與非線性趨勢而設計的統計預測模型，適合應對不規則或長週期時間序列。

多步預測策略（Multistep ahead forecasting strategies）

Multistep ahead forecasting strategies 是指在進行時間序列預測時，如何設計輸入資料的結構、模型的訓練流程，以及最後輸出預測值的方式。

你可以把它理解為在實際開發深度學習或機器學習模型時，所採用的資料切分策略、訓練方法與預測架構。

有幾種常見且實用的策略

遞迴策略（Recursive strategy）

Recursive strategy 目標是根據過去 $d$ 個觀測值，預測未來 $H$ 個時間點的值，這決定了資料每一次遞迴的長度

因為是單輸出策略，每一次的預測，都將受到前面的影響，這包括了預測值，因此，這個策略的缺點是它會嚴重受到誤差積累的影響

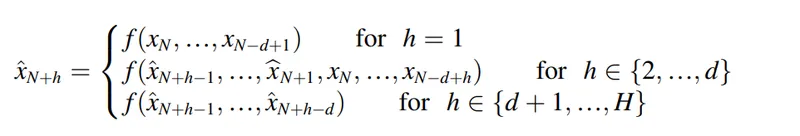
Seasonal recursive strategy

Seasonal recursive strategy 主要特色是，它包含了k個季節延遲，使模型捕捉季節性的變化，並減少 recursive strategy 積累誤差問題

季節性遞迴策略中，前面與一般遞迴一樣，而後半部則包含所有對應的季節數

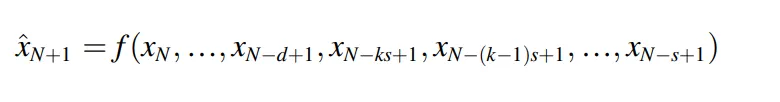
MIMO 策略

MIMO 策略是多輸入多輸出的架構，因此不會像 Recursive strategy（遞迴策略） 那樣面臨預測誤差積累的問題

在這個研究中，MIMO 策略使用在 LSTM 與 MLP 模型

MIMO的缺點是，當資料規模龐大時候，模型訓練可能會出現如，計算成本限制、過擬合、缺乏彈性調整

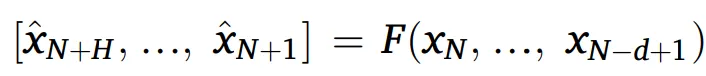
加權平均集成（Weighted Average Ensemble, WAE）

WAE是一個整合預測方法，用來組合多個模型的預測結果，透過加權平均數來進行加總，WAE 的設計可以保留來自不同模型的季節性特徵資訊，特別適合於多重季節性的時間序列預測任務。

公式表示第 $i$ 個模型對未來第 $h$ 小時的預測值，並對每個時間步 $h$ 分別進行加權

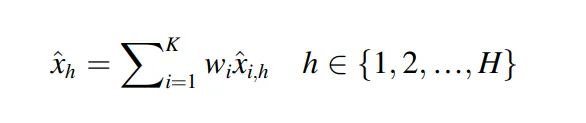
$W_i$ 加權的原理就是該模型的準確度除以所有模型的準確度，也就是加權平均數

表現衡量指標（Performance measures）

回顧基礎 RMSE（均方根誤差）與 MAE（平均絕對誤差）是回歸任務中最常使用的指標

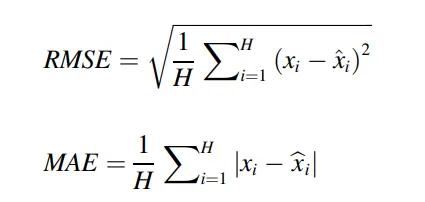
而這兩者都是與資料尺度相關（scale dependent）的，因此不適合用來比較多條不同尺度的時間序列。原因是它們依賴於時間序列本身的數值大小，因此無法準確反映模型的預測效果。

相對性衡量指標 (RelMAE)

該研究建議使用相對性衡量指標（relative measures,RelMAE），原因是當存在多個樣本外預測時，預測範圍（forecast horizon）必須足夠大。

RelMAE指標的特性為尺度獨立（scale-independent）、對稱的（symmetric）、容易解釋的（easily interpretable），即使是對於間歇性時間序列（intermittent time series），也很少會出現異常值的情況。

RelMAE 的定義如下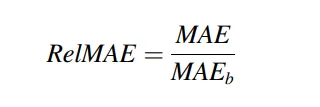： 當 RelMAE > 1 時，表示基準模型的表現優於被評估模型；當 RelMAE < 1 時，則表示被評估模型表現較佳。

此外，本文建議使用 naïve 或 seasonal naïve 方法作為基準模型

結果評估

圖 a 表示了每個模型被選 WAE 選重的次數，總次數為 98 筆店家資料 乘以 5 次 WAE 所選擇的最佳模型，在這裡可以看到常被選擇的模型有 MLP、Mutiple Naive 、HistGB、Prophet、TBATS

圖 b 為 boxplot 來表示每個模型的在WAE中的權重表現，例如整體可以看出 MLP 、HisGB 整體表現中上，且沒有太多極端值，表現相較穩定，而像是 Prophet 有時出現了異常高權重與異常低的權重

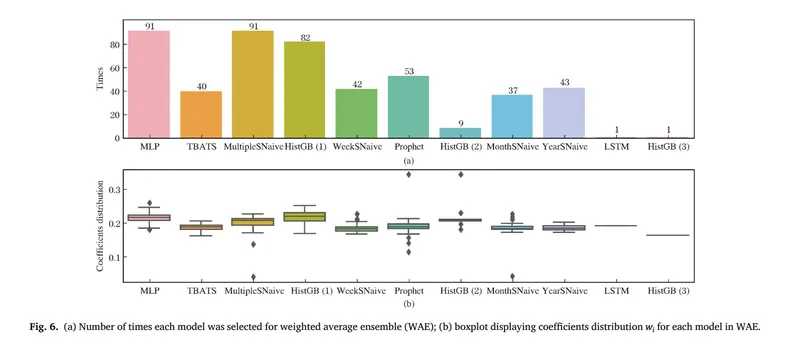
圖7、8中表示，各個模型的單獨的表現結果與真實值得比對，The model was evaluated on the validation set in the second week of November 2019，真實值為紫色，如果模型預測結果與真實值重疊越緊密，表示該預測越準確

其中表現最差為 LSTM，其次為HistGB 2 和 3

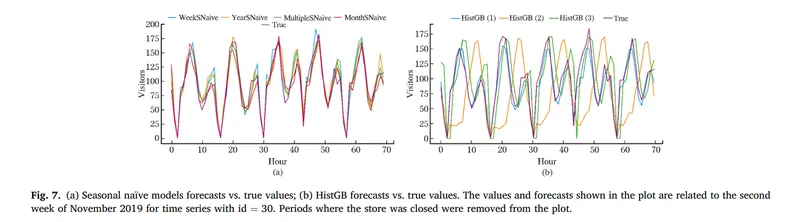
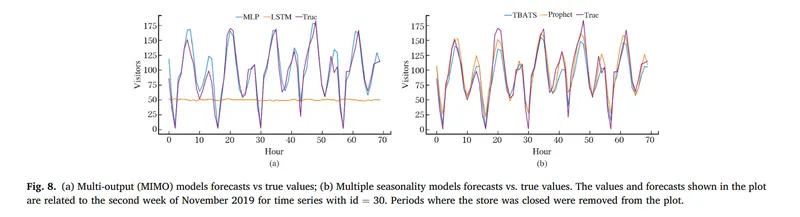
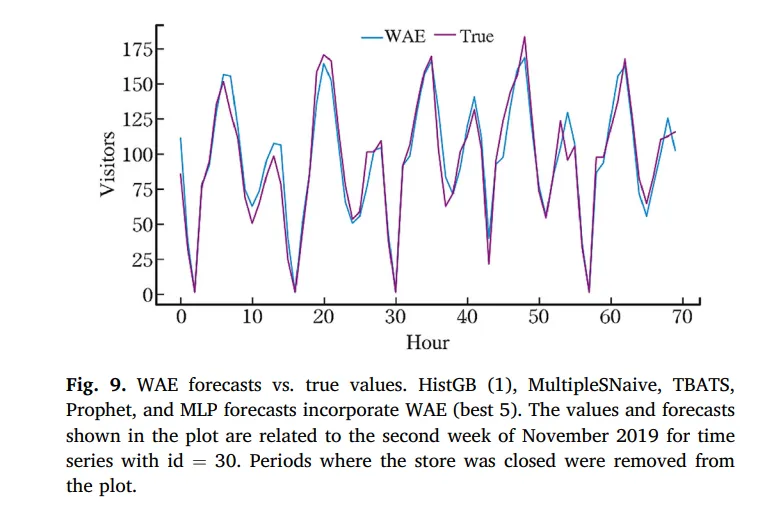
圖9 表示了WAE與真實值，可以看到WAE己乎吻合了真實值，達到穩定的預測品質

這個表格表示了WAE與其他模型單獨預測的表現，你可以看到圖表中的結果，WAE有著最低的誤差值0.742，並且在總資料98筆中勝出了55次，為所有模型中最好的表現