卷積神經網絡-初版 (Convolutional Neural Networks, CNN)

簡序

本篇為卷積神經網路(convolutional neural network，CNN)的研究紀錄，如今網路上已有許多優質的CNN介紹文章，因此本文將直接聚焦在CNN每個的階段流程來進行研究紀錄。

研究方向

1. CNN 基本原理
2. CNN 程式碼運行原理

學前參考

人工智能許多部份都是屬於黑箱模型(Black Box Model)，因此使用更多科學的方法來進行調整與觀察，而許多複雜的理論函數，都已經被包裝成一段函式方法供開發者使用，函數內部如何工作屬於科研方面的範疇。

黑箱模型: 黑箱模型在電腦科學領域中指的是只能了解輸入，但無法輕易知道內部運作，例如在CNN中即便能用數學矩陣以及微積分推導和理解過程，但是當軟體數據規模龐大且變數複雜，即便拆解數學推導過程，也不一定具備可解釋性。

簡易實作

如果需求是為敏捷開發功能應用導向為主，那麼這裡提供一個基本的CNN模型範本，只需要調整參數就能獲得功能來做使用。

程式碼展示: GitHub 連結

運行結果:

elism_threads for best performance.
Epoch 1/10
240/240 - 52s - loss: 0.5044 - accuracy: 0.8526 - val_loss: 0.1444 - val_accuracy: 0.9571 - 52s/epoch - 217ms/step
Epoch 2/10
240/240 - 51s - loss: 0.1448 - accuracy: 0.9554 - val_loss: 0.0930 - val_accuracy: 0.9730 - 51s/epoch - 211ms/step
....
Epoch 9/10
240/240 - 6s - loss: 0.0450 - accuracy: 0.9854 - val_loss: 0.0399 - val_accuracy: 0.9872 - 6s/epoch - 27ms/step
Epoch 10/10
240/240 - 6s - loss: 0.0413 - accuracy: 0.9870 - val_loss: 0.0401 - val_accuracy: 0.9878 - 6s/epoch - 26ms/step
313/313 [==============================] - 1s 3ms/step - loss: 0.0315 - accuracy: 0.9886

準確率= 0.9886000156402588

 Mnist_cnn_model.h5 模型儲存完畢

elism_threads for best performance.
313/313 [==============================] - 1s 3ms/step - loss: 0.0315 - accuracy: 0.9886

準確率= 0.9886000156402588
313/313 [==============================] - 1s 3ms/step
313/313 [==============================] - 1s 2ms/step
預測結果: 7, 真實標籤: 7
預測結果: 2, 真實標籤: 2
...
預測結果: 5, 真實標籤: 5
預測結果: 9, 真實標籤: 9

CNN 基本原理

卷積層 (Convolution Layer)

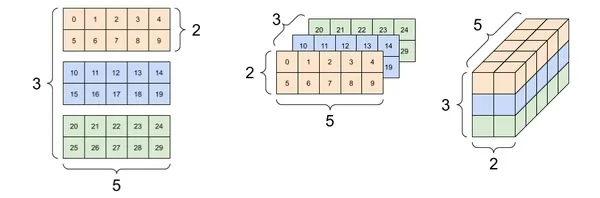
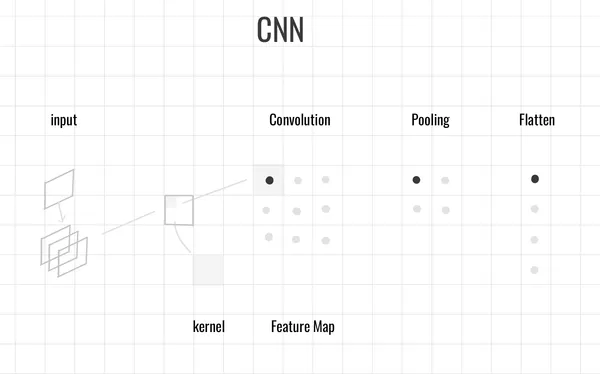
卷積層負責從輸入數據中提取特徵，當卷積層接收圖片時，圖片可以用張量表示。例如，(5 × 2 × 3) 代表一張5 × 2張量、有 3 個通道（例如 RGB 三個顏色通道）的圖片。

卷積核（Kernel / Filter）

是小型矩陣，用來檢測圖片的特徵，例如邊緣或紋理。它會在圖片上滑動（進行卷積運算），並產生 特徵圖（Feature Map），這個卷積核的大小定義皆為開法者設計。

步幅（Stride）

指的是卷積核每次滑動的距離，越大的步幅會讓輸出圖變小，但計算更快，較小的步幅則能保留更多細節。

激活函數 (Activation Function)

在CNN中不管是在卷積層，或是全連接層，都有不同的函數可以處理不同問題，例如ReLU函數可以讓神經網絡能夠學習複雜的模式，解決梯度消失問題，使模型能夠學習更深層的特徵。

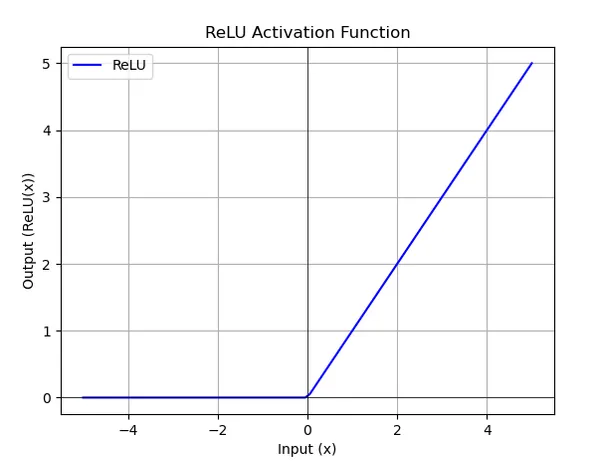
非線性激活函數（ReLU）

ReLU 函數將負數輸出為零，正數保持不變，即保留正數，讓模型能夠學習到更複雜的特徵，解決梯度消失問題。

$$ReLU(x) = \max(0, x)$$

---

池化層 (Pooling Layer)

池化層的作用是 降低特徵圖的維度，減少計算量並提升模型的泛化能力。也有專案選擇不加池化層，以保留更多資訊特徵，取決於開發考量。

常見的池化函數

• 最大池化（Max Pooling）

  最大池化選擇範圍內的最大值，以保留最重要的特徵。

  $$\max(1,2,3,4) = 4$$

  在白話一點的說，可以想像找出圖片最顯眼的特徵表現

• 平均池化（Average Pooling）

  平均池化則計算範圍內數值的平均值，適用於某些需要平滑處理的情境。

  $$average(1,2,3,4)→2.5$$

  白話一點的說，找平均值就像圖片的色塊柔邊處理

---

全連接層 (Fully Connected Layer)

負責將來自卷積和池化層的特徵轉換為最終輸出，並進行特徵分類。

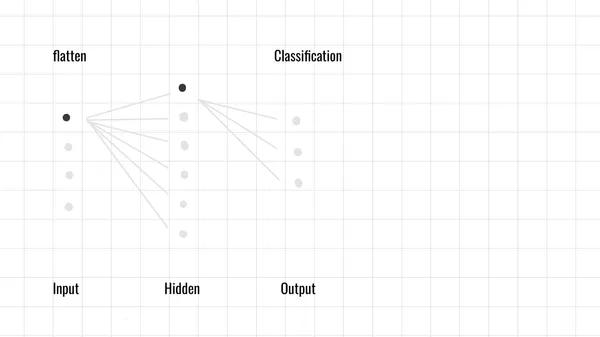
輸入層（Input Layer）

輸入層負責接收來自 卷積層 或 池化層 所提取到的特徵，並將他進行展開(flatten)，也就是將一個三維矩陣 （如高度 × 寬度 × 通道數）變成1維向量。

隱藏層（Hidden Layers）

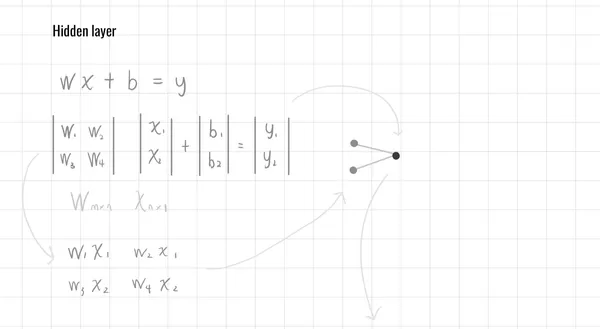
由多個神經元組成，每個神經元會將參數進行加權求和，在通過激活函數來進行調整，最後完成輸出總和 $y$

隱藏層也可以有多層，多層的網絡能夠學習更加抽象的特徵，每增加一層隱藏層，模型的表達能力會顯著增強，使其能夠捕捉到更複雜的模式。

公式表達:

$$y = f(W X + b)$$

• W 為權重矩陣 (設計權重矩陣大小$W_{m*1}$)
• f(x) 為激活函數（如 Sigmoid、Softmax）
• X 為輸入矩陣 (如 Flatten特徵向量所輸入)
• b 為偏置項 (調整參數)
• y 為輸出結果 (使用函數來分類)

輸出層（Output Layer）

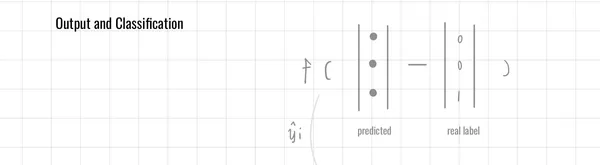
常見函數

多分類問題

使用 Softmax 函數，輸出每個類別的機率

$$\hat{y}_i = \frac{e^{z_i}}{\sum_{j=1}^{C} e^{z_j}}, \quad i=1,\ldots,C$$

• $\hat{y_i}$ 為預測權重，為一個連續的結果

二元分類問題

使用 Sigmoid 函數，二元問題意味著合格與不合格等等判別

$$\hat{y} = \frac{1}{1+e^{-z}}$$

• $\hat{y}$ 為預測權重

前向傳播（Forward Propagation）

前向傳播指的是從輸入層→隱藏層→輸出層的一個流程，也就是到目前為止的流程，可以先知道前向傳播的意思，因為後續會有一個相對應的流程稱為反向傳播（Backpropagation,BP）。

損失函數

損失函數主要為了計算「預測值」與「正確的標籤」存在多少誤差，當輸出層輸出結果後，會拿取預測值在與真實標籤來比較，量化這個差距的數值稱為損失函數

例如

在Tensorflow模型每次(Epoch )訓練階段完成時可以看到損失函數，透過觀察損失函數變化，來了解模型當前的訓練狀況，損失函數每次結果越小則模型表現越佳。

Epoch 1/10
240/240 - 52s - loss: 0.5044 - accuracy: 0.8526 - val_loss: 0.1444 - val_accuracy: 0.9571 - 52s/epoch - 217ms/step

函數常見的有:

• 平均絕對誤差（MAE，Mean Absolute Error）：計算預測值與真實值之間差異的絕對值平均。
• 均方誤差（MSE，Mean Squared Error）：計算預測值與真實值之間差異的平方平均。
• 交叉熵（Cross-Entropy）：常用於分類問題，衡量預測的概率分佈與真實分佈之間的差異。

反向傳播（Backpropagation,BP）

當結束向前傳播流程後，即來到反向傳播，先是計算損失函數求得梯數，在通過調整網絡中的權重，讓預測結果更接近真實值

梯度 (Gradient)

梯度是向量微積分 ( Vector calculus）中的概念，也用作多元微積分 (Multivariable calculus)，為了先繼續聚焦在神經網路中的主題，在這部分先初步理解梯度表示與特性，這裡的梯度為偏導數以及多維(multi-dimensional)概念

梯度表示

$$\operatorname{grad}(f) = \nabla f$$

以及一個梯度的例子

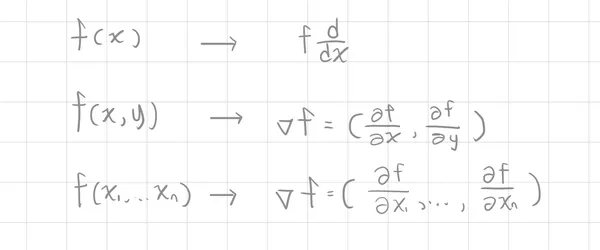
梯度下降（Gradient Descent）

是損失函數對參數的偏導數，目標是最小化損失函數（Cost Function），或預測值與真實值之間的誤差，讓模型的預測結果更接近真實值。

使用優化器（Optimizer）根據梯度更新權重：

$$\theta = \theta - \eta \cdot \nabla_\theta L(\theta)$$

其中：

• $\theta$ 是當前的權重參數
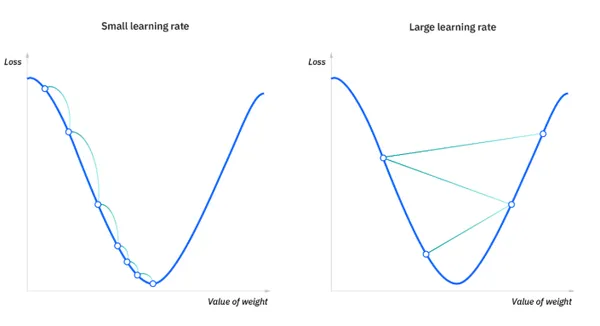
• $\eta$ 是學習率（learning rate）
• $\nabla_\theta$ L($\theta$) 是損失函數對權重的梯度，表示當前權重對損失的影響

梯度存在問題

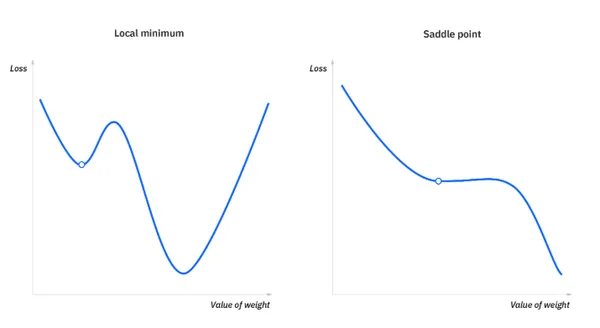
局部最小值和鞍點 ( Local minima and saddle points )

為了要達到模型最佳化，要解決凸點最佳化問題 (Convex optimization problems)，目標是找到全局最小值 (global minimum)，而不要被困在區域最小值 (local minimum)

梯度消失（Vanishing Gradient）

隨著神經網路的層層運算，某些層的梯度可能會越來越小，導致學習效果緩慢或停止，套用模擬神經元的設計構想，當部分權重參數趨近於零或歸零，也可稱為神經元死亡，為了解決這個問題使梯度從原本的線性問題調整為非線性問題。

解決方法：

使用 ReLU 激活函數（避免梯度消失）或 批次正規化（Batch Normalization）

梯度爆炸 (Exploding gradients)

梯度逐漸變大，可能導致權重更新過大，模型不穩定，解決這部分問題則稱為降維(dimensionality reduction)。

難免有錯誤，歡迎幫忙檢視改正

文章發布出處

卷積神經網絡-初版 (Convolutional Neural Networks, CNN). 36號系統. https://r036.blog/software/artificial-intelligence/AI20250003

參考文獻

[1] Vector Calculus: Understanding the Gradient(n.d.). Better Explained. https://betterexplained.com/articles/vector-calculus-understanding-the-gradient/

3Blue1Brown: But what is a neural network?

What Is Gradient Descent? (n.d.). IBM. https://www.ibm.com/think/topics/gradient-descent

What is learning rate in machine learning?(n.d.). IBM. https://www.ibm.com/think/topics/learning-rate

An overview of gradient descent optimization algorithms(n.d.). ruder.io. https://www.ruder.io/optimizing-gradient-descent/