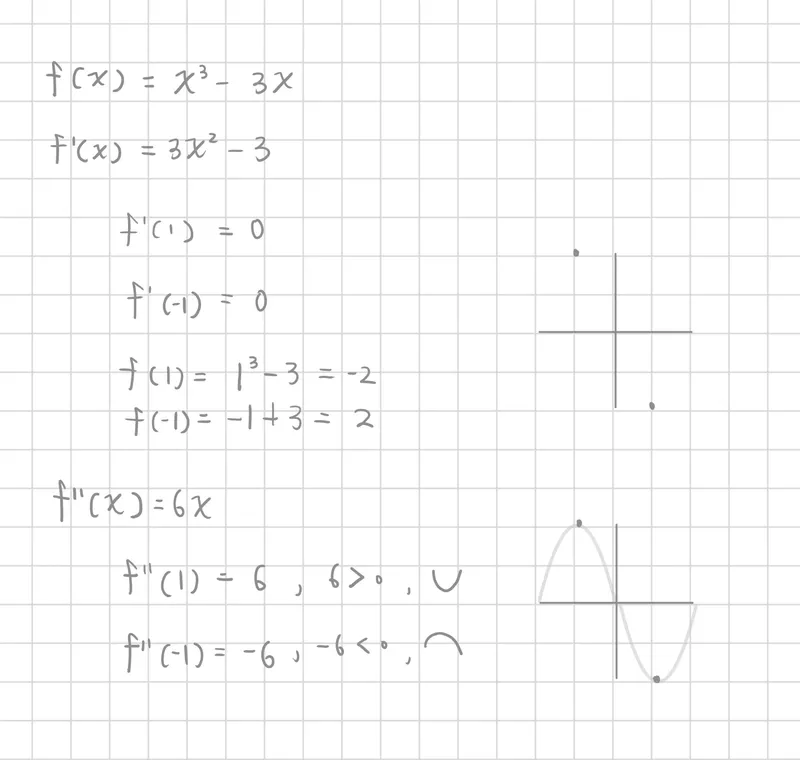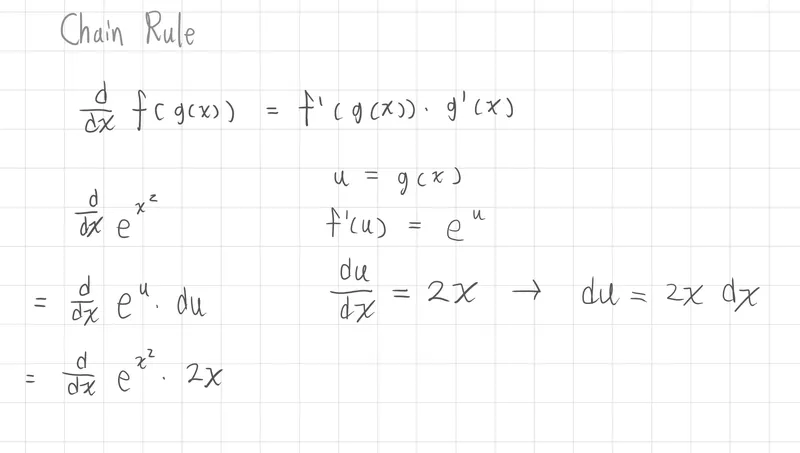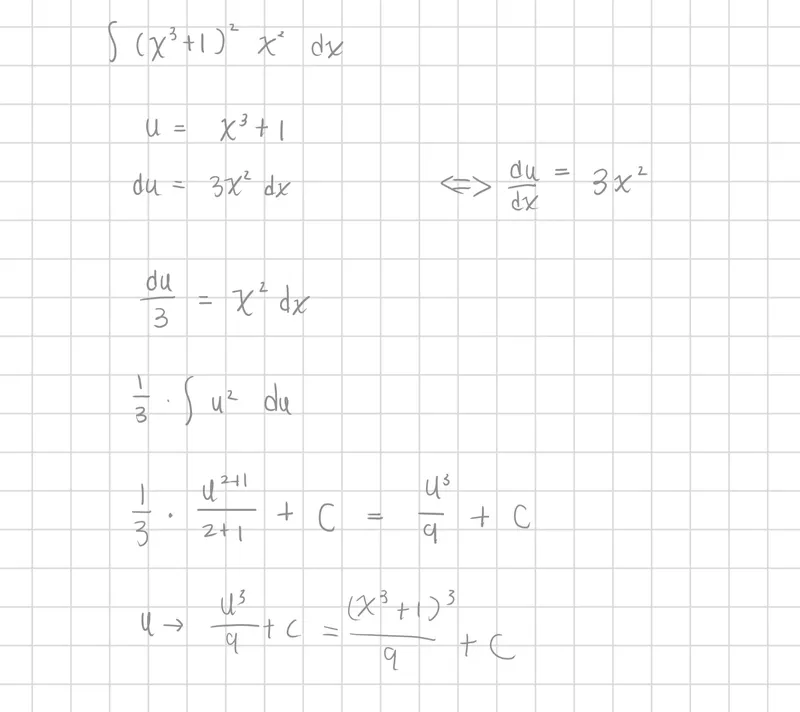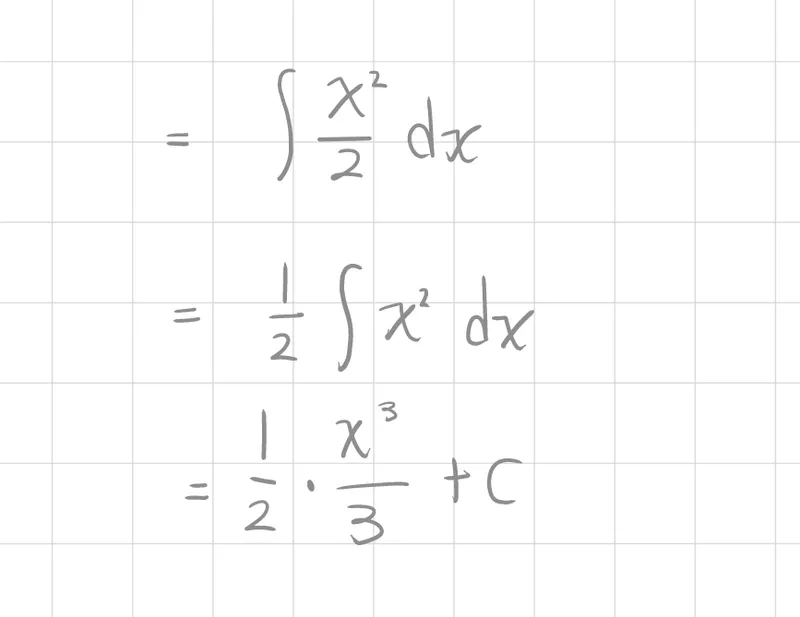微積分-電腦科學應用數學
前敘
筆記內容著重於,電腦科學與人工智慧領域所應用的數學,目的為快速導讀重點脈絡及公式,類似於直式的心智圖,有助於構思規劃學習路線,或是直接查找應用。
目錄
筆記目前整理部分
-
微積分
(研究連續變化、累積與極限現象的數學,應用於函數分析、優化與動態系統建模)
-
線性代數
(研究向量、矩陣與線性變換的結構與操作,為機器學習與深度學習的核心基礎)
-
離散數學(廣義邏輯學)
(研究離散結構與邏輯基礎,包含集合論、圖論、布林代數等,支撐演算法設計與計算理論)
-
統計學
(研究資料分佈、推論與估計,是資料分析與機器學習模型評估的重要工具)
-
幾何學
(研究形狀、空間關係與度量,在電腦視覺、圖形學與機器人定位中應用廣泛)
-
數學分析
(研究極限、收斂性與嚴格定義的連續性,是微積分的理論基礎並延伸至泛函分析)
-
機率論
(研究隨機事件與不確定性,為貝葉斯推論、馬可夫過程及強化學習等提供理論支撐)
導數 (derivatives)
表達
y=f(x)
f(x)⇒f′(x)
dxdf(x)=f′(x)
極限定義:
f′(a)=x→alimx−af(x)−f(a)
f′(x)=h→0limhf(x+h)−f(x)
一階導數
找到臨界點
- 求出一階導數 f′(x) 並解 f′(x) 找到臨界點(Critical points)
- 判斷增減趨勢:
在臨界點的左右區間內取不同的 x 值,代入 f′(x) 看結果是正還是負
- 如果 f'(x) > 0 ,則該區間內遞增
- 如果 f'(x) < 0,則該區間內遞減
- 如果 f'(x) = 0,則臨界點是極值點
二階導數
確認臨界點的性質
凹性
(tag: 待補充)
- 若 f′′(x)>0,函數在該點凹向上,可能為極小值。
- 若 f′′(x)<0,函數在該點凹向下,可能為極大值。
- 若 f''(x) = 0,則無法直接判斷,可能是反曲點或鞍點(Saddle point)
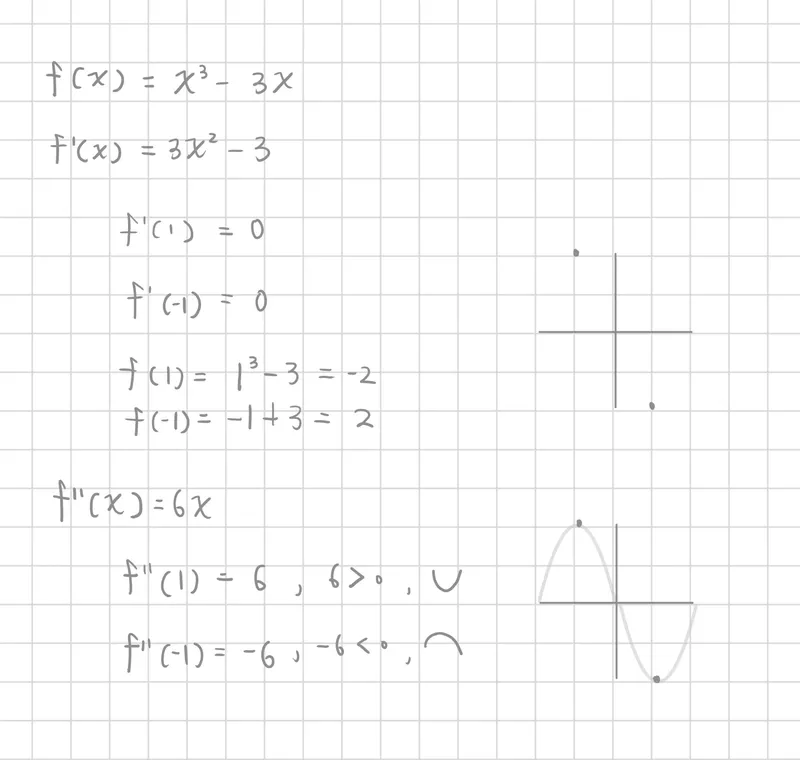
導數運算規則
-
導數的定義
- 導數 dxdu 表示 u 隨 x 變化的瞬時變化率。
-
微分的定義
冪函數
dxdxn=nxn−1
對數函數
dxdlnx=x1
dxdlogax=xlna1
dxdex=ex
dxdlnx=x1
dxdax=axlna
ea⋅eb=ea+b
(ea)b=eab
加法法則
dxd(f(x)+g(x))=f′(x)+g′(x)
乘法法則(Product Rule)
用於微積分導數的乘法計算,而不是基礎數學的乘法運算
y=f(x)⋅g(x)
dxd(f(x)g(x))=f′(x)g(x)+f(x)g′(x)
y′=f′(x)g(x)+f(x)g′(x)
商法則(Quotient Rule)
dxd(g(x)f(x))=g2(x)f′(x)g(x)−f(x)g′(x)
鏈鎖法則(Chain Rule)
dxdf(g(x))=f′(g(x))g′(x)
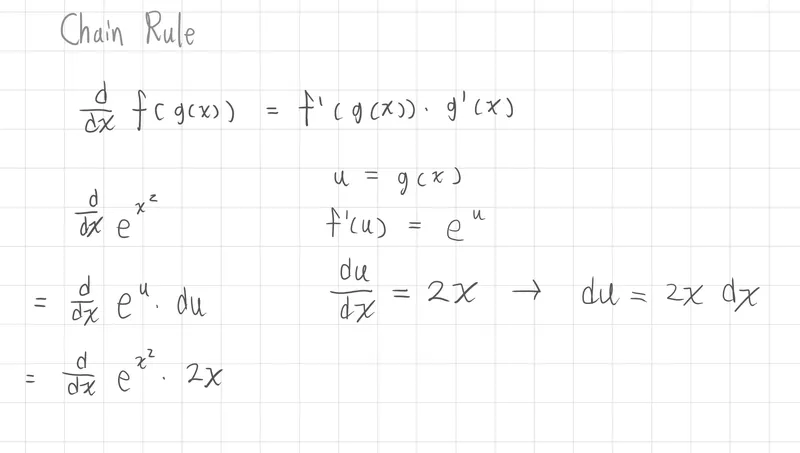
偏微分
// 在深度學習梯度下降時使用到偏微分
例如,考慮一個有兩個變數 f(x,y) 的函數:
f(x,y)=x2+y2
若我們對 x 進行偏微分,我們將 y 視為常數,得到:
∂x∂f=2x
同樣地,若對 y 進行偏微分,我們將 x 視為常數,得到:
∂y∂f=2y
不定積分(Integration)
常數項:
∫cdx=cx+C
幂函數(n=−1):
∫xndx=n+11xn+1+C
指數函數:
∫exdx=ex+C
三角函數:
∫sinxdx=−cosx+C,∫cosxdx=sinx+C
倒數積分
∫x1dx=ln∣x∣+C
代換積分(Substitution Rule)
∫f(g(x))g′(x)dx=∫f(u)du,u=g(x)
適用於變數替換 u=g(x)
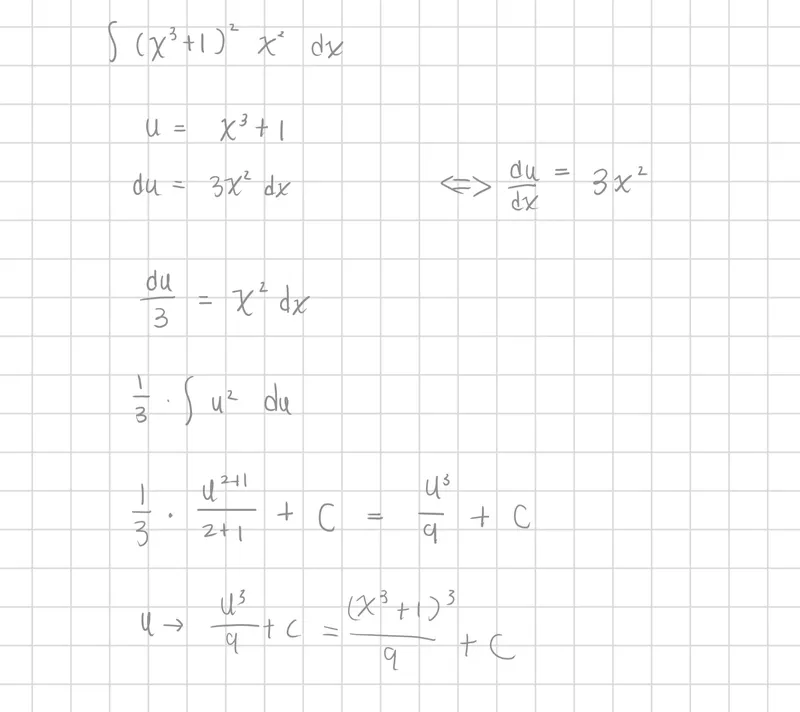
係數乘法(Constant Multiple Rule)
∫kf(x)dx=k∫f(x)dx
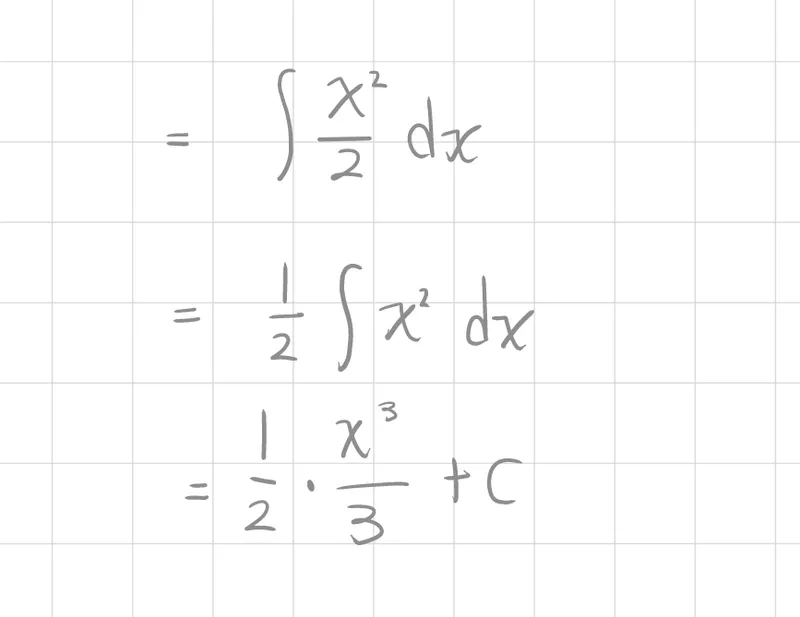
∫udv=uv−∫vdu
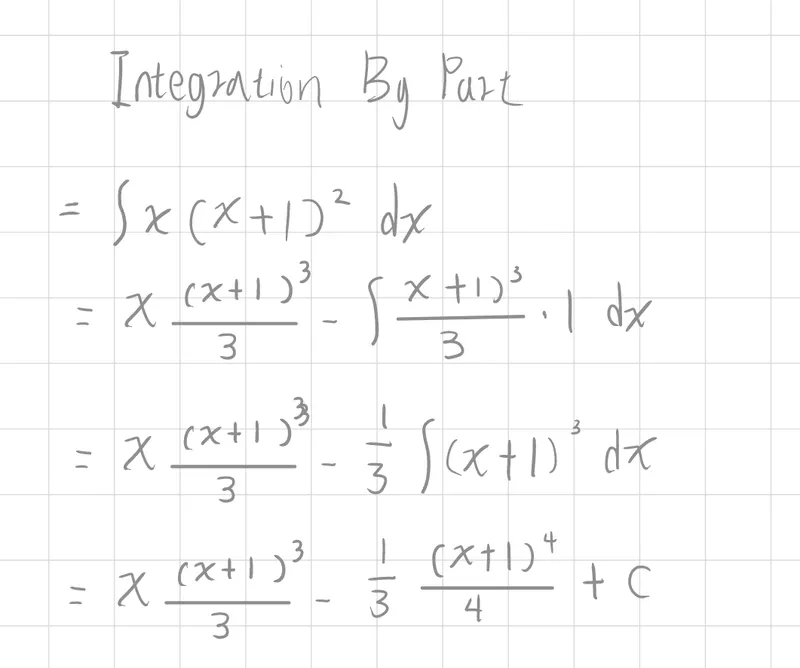
定積分(definite integral)
基本性質
∫aaf(x)dx=0
∫abf(x)dx=−∫baf(x)dx
牛頓-萊布尼茲定理
若 F(x) 是 f(x)的不定積分:
∫abf(x)dx=F(b)−F(a)