幾何學

前敘

筆記內容著重於，電腦科學與人工智慧領域所應用的數學，目的為快速導讀重點脈絡及公式，類似於直式的心智圖，有助於構思規劃學習路線，或是直接查找應用。

---

目錄

筆記目前整理部分

• 微積分
  (研究連續變化、累積與極限現象的數學，應用於函數分析、優化與動態系統建模)

• 線性代數
  (研究向量、矩陣與線性變換的結構與操作，為機器學習與深度學習的核心基礎)

• 離散數學（廣義邏輯學）
  (研究離散結構與邏輯基礎，包含集合論、圖論、布林代數等，支撐演算法設計與計算理論)

• 統計學
  (研究資料分佈、推論與估計，是資料分析與機器學習模型評估的重要工具)

• 幾何學
  (研究形狀、空間關係與度量，在電腦視覺、圖形學與機器人定位中應用廣泛)

• 數學分析
  (研究極限、收斂性與嚴格定義的連續性，是微積分的理論基礎並延伸至泛函分析)

• 機率論
  (研究隨機事件與不確定性，為貝葉斯推論、馬可夫過程及強化學習等提供理論支撐)

---

直線方程式(Equations of Straight )

給定方程式：y=5x

• x 代表工作小時數。
• y 代表賺取的總工資

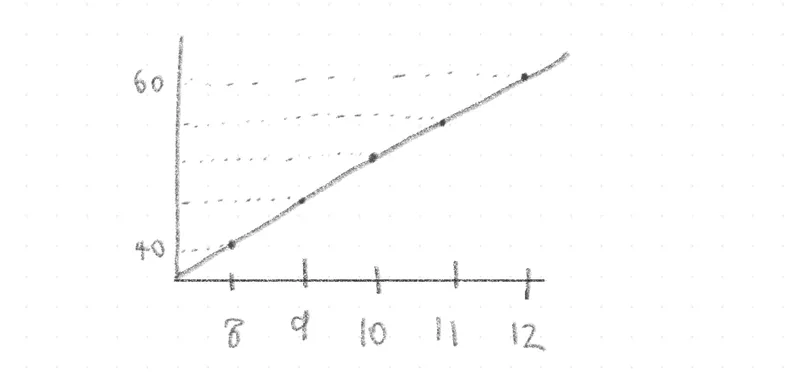
斜率（slope）

斜率（$m$）確實是兩點之間的變化率，表示的是垂直變化相對於水平變化的比例

而向量則同時具有大小和方向

$$m = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}$$ $$m = \frac{60 - 40}{12 - 8} = \frac{20}{4} = 5$$

斜截式（Slope-Intercept Form）

可以透過 $b$ 來找到直線在 $y$ 軸上的交點

$$y=mx+b$$

可以轉換為一般式：

$$-mx + y - b = 0$$

代入已知點 $(8,40)$ 求出方程式，並求得截距 b

$$40=5(8)+ 0$$

兩點式/點斜式（Point-Slope Form）

重點: 一個點 $(x_1, y_1)$ 與m 求得方程式

$$y - y_1 = m(x - x_1)$$

可以轉換為一般式：

$$-m (x - x_1) + (y - y_1) = 0$$

帶入已知條件 $x_1, y_1, m$ 為必須通過的點

$$(x1,y1)=(0,0)\\.\\ y−0=5(x−0)\\ y=5x$$

截距式 (Intercept Form)

$$\frac{x}{a} + \frac{y}{b} = 1$$

如果一條直線穿過 x 軸的 a=4和 y 軸的 b =6

$$\frac{x}{4} + \frac{y}{6} = 1$$

轉換一般式，兩邊同乘 12 消去分數

$$3x+2y=12$$

再移項得到一般式

$$3x+2y−12=0$$

畢氏定理（Pythagorean Theorem）

畢氏定理描述的是在直角三角形中，斜邊的平方，等於兩個直角邊的平方和

$$c^2 = a^2 + b^2$$

• $c$ 是斜邊的長度

• $a$ 和 $b$ 是直角邊的長度

在數學和統計中，希臘字母 $\mu$（讀作 mu）非常常見，常見用途如下：

三角函數（Trigonometric Functions）

單位圓定義

$$P(\theta) = (\cos\theta, \sin\theta)$$

• $\sin\theta = y$，$\cos\theta = x$
• $\tan\theta = \dfrac{y}{x}$（當 $x \neq 0$）

---